Программа расчета "Метод главных компонент"

На практике в предположении малости s² для e_i изучают корреляционную матрицу Â  для  исходных  величин Х.

Как уже отмечалось, матрицу Â можно связать с матрицей факторных нагрузок: Â = W ^.W '.

Учитывая, что Â- симметричная положительно определенная матрица, представим ее в виде  Â = ULU', где U - ортогональная матрица собственных векторов матрицы Â, а L - диагональная матрица собственных чисел матрицы Â. Тогда, сравнивая два последних равенства, имеем W = =U× L^1/2.

Теперь, учитывая, что Y = WХ, можно вычислить матрицу Y главных компонент, для которой l_i являются дисперсиями соответствующих компонент.

Система собственных векторов U является ортогональной, а из ортогональности следует их некоррелированность. Иными словами, корреляционная матрицы Â оказывается в результате расщепленной на N ортогональных некоррелированных компонент.

Традиционноl_i располагают в порядке убывания, т.е. l₁ соответствует самое большое значение из l_i, которое называют первой главной компонентой. Второе значение l₂ - второй главной компонентой. Метод построения комбинацией вида Y = WХ называется компонентным анализом, или методом главных компонент.

Геометрически определение главных компонент приводит к новой ортогональной системе координат. Причем первая координатная ось вычисляется таким образом, чтобы соответствующая ей линейная форма извлекала возможно большую дисперсию. Далее находится ортогональная этой форме ось, которая делает то же самое с оставшейся дисперсией. И так далее, т.е. в N-мерном пространстве величин Х₁,..., Х_N ось наибольшей протяженности N-мерного эллипсоида рассеяния Х_N определится направляющими косинусами, равными компонентам вектора W.

Проекция Х на направление w₁ имеет наибольшую дисперсию по сравнению с их проекциями на другие направления. Кроме того, учитывая ортогональность системы W, можно перейти к старым координатам 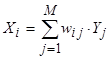, где Y_j - j-я главная компонента; w_ij - вес i-й компоненты в j-й случайной величине.

Последнее соотношение - основное в МГК. Оно не содержит остаточной составляющей e и получается, что все N_j главных компонент исчерпывают всю дисперсию исходных данных. В МГК поэтому нет необходимости делать какие-либо предположения, величины Х_i даже не обязательно считать случайными. Единственным недостатком рассматриваемого метода является то, что главные компоненты неинвариантны относительно изменения масштаба тех шкал, по которым отсчитываются разные случайные величины.

Именно поэтому анализ МГК целесообразно использовать тогда, когда все Х_i измерены в одних и тех же единицах. Для этого обычно берут либо нормированные данные , либо приводят экспериментальные данные к нормальному распределению. Однако надо заметить, что ни первый, ни второй приемы не имеют строгого математического обоснования.

На практике обычно для оценки количества независимых факторов оставляют только те l_i , которые в сумме дают 90 - 95 % от всех l_i . Количество оставшихся собственных значений и дает оценку числа независимых факторов. Чаще всего сохраняют все l_i > 1, т.е. только дающие  наибольший вклад в дисперсию.

Алгоритм, реализующий МГК, может быть записан следующей вычислительной схемой:

1. Вычислить матрицу взаимных корреляций Â для экспериментальных данных Х.

2. Пользуясь любым методом, вычислить собственные значения матрицы Â(l_i ).

3. Определить матрицу факторных нагрузок W.

4. Найти матрицу главных компонент Y.

5. Выделить у_i , соответствующие l_i , которые в сумме дают не менее 95 % от всей суммы  .

6. Пересчитать Х_i в соответствии с оставшимися факторами, получить новую матрицу Х⁽¹⁾.

7. Проанализировать матрицы W, Y и новую матрицу Х⁽¹⁾ с целью выделения групп.

При программировании МГК целесообразно пункты1, 2 и 3 оформить отдельными процедурами. Матрицу Â лучше вычислять из ковариационной матрицы для уменьшения вычислительной погрешности.

По процедуре СОRR вычисляется матрица Â взаимных корреляций (взять