Интегрирование с автоматическим выбором количества узлов

В ряде задач, например при численном решении эволюционных интегродифференциальных уравнений высокого порядка, когда вычисление определенного интеграла должно выполняться на сетке с изменяющимся от шага к шагу количеством узлов квадратурной формулы (переменные находятся “внутри” функционирующего алгоритма, применяется один или несколько пределов интегрирования), а порядок аппроксимации должен при этом соответствовать порядку разностной схемы для дифференциальной части уравнения, возникает весьма нетривиальная проблема автоматического выбора количества узлов квадратурной формулы, имеющей достаточно высокую точность [Белашов, 1989, 1991a, б, 1997]. Рассмотрим в качестве примера, каким образом могут в этом случае использоваться такие известные квадратурные формулы, как Симпсона и Ньютона-Котеса с количеством узлов m>3.

Пусть, например, уравнение имеет вид

                                                   (3.9)

где  - некоторый дифференциальный оператор;  f  - интегральный член, и пусть порядок аппроксимации дифференциальной части уравнения (для простоты будем считать его двумерным по пространственным координатам) . В этом случае для аппроксимации его интегральной части f достаточно выбрать квадратурную формулу Симпсона

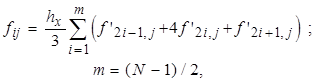             (3.10)

(- аппроксимация соответствующей подынтегральной функции, N - нечетное), которая согласно оценкам, полученным Белашовым [1989, 1991б], аппроксимирует интеграл на решениях уравнения (3.9) с точностью  для шагов сетки h_x,h_y £ 0.075 (зависит от постоянных коэффициентов уравнения). Меньшие требования к размеру шага и расположению узлов пространственной сетки имеют аппроксимации интеграла квадратурными формулами Ньютона-Котеса с количеством узлов m >3:

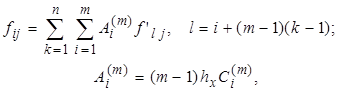 (3.11)

где - коэффициенты квадратурной формулы. При этом следует помнить, что m должно выбираться таким, чтобы выражение (N - 1) / (m - 1) было целым. Аппроксимация (3.11) позволяет вычислять интеграл f  с точностью  уже для  h_x,h_y £ 0.1 [Белашов, 1989].

Ограничение на шаг по времени, которое дают формулы (3.7), (3.10), при учете двумерности задачи весьма существенно. Кроме того, на каждом временном слое требуется запоминать значения функции на двух предыдущих слоях. Поэтому такие сравнительно простые схемы, как (3.2) и (3.8), вряд ли целесообразно использовать для получения решения в асимптотике . Однако они могут оказаться полезными для моделирования динамики становления решения на начальной стадии эволюции.

Ниже приводится подпрограмма fnk, использующая функцию ku, которая осуществляет автоматический выбор квадратурной формулы из семейства формул Ньютона-Котеса в зависимости от количества узлов сетки, и вычисляющая соответствующий интеграл.

Формальные параметры процедур. Входные: p - одномерный (real) массив значений подынтегральной функции размерностью N; h (тип real) - шаг сетки. Выходные: функция fnk возвращает вычисленное значение интеграла.

FUNCTION FNK ( P : ARRAY OF REAL;

K, N : INTEGER; H: REAL) : REAL;

VAR C,C8 : ARRAY [1..8] OF REAL;

C2 : ARRAY [1..2] OF REAL;

C3 : ARRAY [1..3] OF REAL;  

C4 : ARRAY [1..4 OF REAL;

C5 : ARRAY [1..5] OF REAL;

C6 : ARRAY [1..6] OF REAL;

C7 : ARRAY [1..7] OF REAL;

NA, I, J, NJ, N1, D, NZ, JJJ, III : INTEGER;

F : REAL;

FUNCTION KU ( VAR N : INTEGER) : INTEGER;

VAR N1, J, I, ND : INTEGER;

BEGIN

N1:=N-1;

FOR I := 1 TO 7 DO

BEGIN

J := 8 - I;

ND := MOD (N1, J);

IF ND := 0 THEN

BEGIN

KU := J + 1;

EXIT;

END;

END;

KU := J + 1;

END;

BEGIN    C2 [1] := 0.5;

C2 [2] := 0.5;

C3 [1] :=0.1666667;

C3 [2] :=0.6666667;

C3 [3] :=0.1666667;

C4 [1] := 0.125;

C4 [2] := 0.375;

C4 [3] := 0.375;

C4 [4] := 0.125;

C5 [1] := 0.0777778;

C5 [2] := 0.3555556;

C5 [3] := 0.1333333;

C5 [4] := 0.3555556;

C5 [5] := 0.0777778;

C6 [1] := 0.0659722;

C6 [2] := 0.2604167;

C6 [3] := 0.1736111;

C6 [4] := 0.1736111;

C6 [5] := 0.2604167;

C6 [6] := 0.0659722;

C7 [1] := 0.0488095;

C7 [2] := 0.2571429;

C7 [3] := 0.0321429;

C7 [4] := 0.3238095;

C7 [5] := 0.0321429;

C7 [6] := 0.2571429;

C7 [7] := 0.0488095; 

C8 [1] := 0.0434606;

C8 [2] := 0.2070023;

C8 [3] := 0.0765625;

C8 [4] := 0.1729745;

C8 [5] := 0.1729745;

C8 [6] := 0.0765625;

C8 [7] := 0.2070023;

C8 [8] := 0.0434606;

NA := N - K + 1;

IF (N - K) <= 0 THEN

BEGIN

F := 0.0;

FNK := F;

EXIT;

END;

NJ := KU (NA);

CASE NJ OF

1 : BEGIN

F := 0.0;    FNK := F;

EXIT;

END;

2 : FOR I := 1 TO NJ

C [I] := C2 [I];

3 : FOR I := 1 TO NJ

C [I] := C3 [I];

4 : FOR I := 1 TO NJ

C [I] := C4 [I];

5 : FOR I := 1 TO NJ

C [I] := C5 [I];

6 : FOR I := 1 TO NJ

C [I] := C6 [I];

7 : FOR I := 1 TO NJ

C [I] := C7 [I];

8 : FOR I := 1 TO NJ

C [I] := C8 [I];

END;  { **** CASE **** }

N1 := NJ - 1;

D   := N1*H;

NZ := NA DIV N1;

IF (NJ - 2) < = 0 THEN NZ := NZ - 1;

F   := 0.0;

FOR J := 1 TO NZ DO

BEGIN

JJJ := N1*(J - 1) + K - 1;

FOR  I := 1 TO NJ DO

BEGIN

III := I + JJJ;

F := F + C[I]*D*P[III];

END;

END;  

FNK := F;

END.

Подпрограмма fnk тестировалась на ЭВМ Pentium-166 для массивов от 21 до 5001 членов. Результаты показали, что подпрограмма обеспечивает заданную точность вычислений при разумных значениях шага сетки h, кроме того, она эффективно использовалась в системе моделирования динамики нелинейных волн в плазме, описываемых уравнениями типа уравнения Кадомцева - Петвиашвили, представленной в серии работ В.Ю.Белашова [Белашов, 1989, 1991a, б, 1997].