Метод Буркова. Анализ корреляционной матрицы методом корреляционных профилей

С некоторой долей условности к иерархическим методам группирования можно отнести метод Ю.К.Буркова [1973], который широко применяется в геохимии и называется также методом многократной корреляции (ММК). Он хотя дает конечные результаты, имеющие иерархическую структуру, но сам характер классифицирующий процедуры заметно отличается от иерархического.

B ММК объединение элементов в классы производится на основе меры сходства, роль которой играют корреляционные моменты высших порядков. Корреляционные моменты рассчитываются на каждом новом шаге по формуле

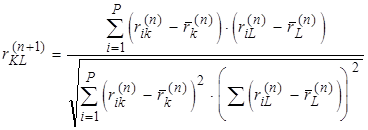, где r_ik, r_iL - компоненты k-го и L-го столбцов матрицы Â*, полученной последовательным преобразованием матрицы взаимной корреляции;  и - средние арифметические числа для k-го и L-го столбцов: 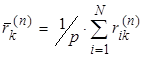; р - размерность матрицы Â*. Как следует из приведенной формулы, суть метода Ю.К. Буркова заключается в отыскании таких групп элементов, которые обладают сходным характером связи как между собой (внутри группы), так и с элементами других групп.

Каждому элементу из множества А поставим в соответствие вектор-столбец исходной корреляционной матрицы Â и обозначим новую матрицу Â⁽¹⁾. Если теперь вычислим взаимный коэффициент корреляции от элементов матрицы Â⁽¹⁾, то получим матрицу Â⁽²⁾. При этом сами  будут превышать исходный коэффициент корреляции , если векторы имеют достаточно уверенную взаимосвязь. В противном случае  > . В целом обнаруживается тенденция: с увеличением количества шагов n величина  стремится либо к +1, либо к -1, причем для некоторых групп значения  достигают +1 уже при n < 4. Если нужно для достижения +1 больше пяти пересчетов матрицы Â, то говорят, что эти элементы не столь тесно связаны в данной группе.

Конечный результат соответствует разбиению матрицы (множества А) на две "антагонистические" ассоциации: элементы а_j, связанные в одной ассоциации, имеют r⁽ⁿ⁾ равное +1, а элементы а_L, связанные в противоположной ассоциации, r⁽ⁿ⁾  равное - 1.

Метод многократной корреляции привлекает простотой алгоритма, но вместе с тем имеет серьезный недостаток. Его нецелесообразно применять в ситуациях, когда есть данные, говорящие о существовании более двух групп связанных элементов, что соответствует действию более чем двух факторов. Однако для прикладных или предварительных расчетов этот метод можно использовать довольно успешно.

Вычислительная процедура, используемая здесь, уже применялась для расчета корреляционной матрицы (глава 7, § 5). Единственное отличие ее состоит в самой вычислительной схеме, т.е. в основной программе. Поэтому для выполнения данной работы можно воспользоваться процедурой расчета корреляционной матрицы без изменений.

Для демонстрации и проверки процедур корреляционная матрица (табл. 8.2) анализируется уже описанным методом. Используются данные из табл. 7.9, по которым ранее строилась корреляционная матрица. Анализ проводится по уровням значимости 0.05 и 0.1. Вычисления выполнены с точностью 10^-5. Результат работы приводится в табл. 8.3. Обозначения сохранены, как в главе 7.

Из анализа матрицы корреляционных профилей видно (табл. 8.3, итерации 4 - 6), что все элементы уверенно разделились на две антагонистические группы: к первой можно отнести элементы I, II, III столбцов, а ко второй IV и V (табл. 8.2). Связь элементов II и III не очевидна, поэтому результат нуждается в дополнительной проверке. Аналогичной проверке необходимо подвергнуть группу II и IV, так как корреляционная матрица дала в указанном случае противоположный результат (по связи элементов). Делая вывод, можно предположить следующую группировку элементов: I - III; IV - V; II. Положение элемента II необходимо уточнить другими методами.

Таблица 8.2

№	I	II	III	IV	V
I	1.00000	0.33842	0.58387**	-0.29250	-0.45483*
II	0.33842	1.00000	-0.05452	0.52663*	-0.45056*
III	0.58387**	-0.05452	1.00000	-0.72840**	-0.73536**
IV	-0.29250	0.52663*	-0.72840**	1.00000	0.36006
V	-0.45483*	-0.45056*	-0.73536**	0.36006	1.00000

Таблица 8.3

	I	II	III	IV	V	I	II	III	IV	V	I	II	III	IV	V
	Итерация первая					Итерация третья					Итерация пятая
I	1.00	0.28	0.89	-0.72	-0.88	1.00	0.49	1.00	-0.98	-1.00	1.00	0.99	1.00	-1.00	-1.00
II	0.28	1.00	0.01	0.39	-0.47	0.49	1.00	0.42	-0.30	-0.55	0.99	1.00	0.99	-0.99	-0.99
III	0.89	0.01	1.00	-0.91	-0.88	1.00	0.42	1.00	-0.99	-0.99	1.00	0.99	1.00	-1.00	-1.00
IV	-0.72	0.39	-0.91	1.00	0.61	-0.98	-0.30	-0.99	1.00	0.96	-1.00	-0.99	-1.00	1.00	1.00
V	-0.88	-0.47	-0.88	0.61	1.00	-1.00	-0.55	-0.99	0.96	1.00	-1.00	-0.99	-1.00	1.00	1.00
	Итерация вторая					Итерация четвертая					Итерация шестая
I	1.00	0.30	0.99	-0.92	-0.99	1.00	0.83	1.00	-1.00	-1.00	1.00	1.00	1.00	-1.00	-1.00
II	0.30	1.00	0.15	0.11	-0.43	0.83	1.00	0.82	-0.79	-0.85	1.00	1.00	1.00	-1.00	-1.00
II	0.99	0.15	1.00	-0.97	-0.96	1.00	0.82	1.00	-1.00	-1.00	1.00	1.00	1.00	-1.00	-1.00
IV	-0.92	0.11	-0.97	1.00	0.85	-1.00	-0.79	-1.00	1.00	0.99	-1.00	-1.00	-1.00	1.00	1.00
V	-0.99	-0.43	-0.96	0.85	1.00	-1.00	-0.85	-1.00	0.99	1.00	-1.00	-1.00	-1.00	1.00	1.00

§ 3. АНАЛИЗ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ                                                 МЕТОДОМ КОРРЕЛЯЦИОННЫХ ПРОФИЛЕЙ

Этот метод известен как метод корреляционных профилей (МКП) Фишера или метод пробных графиков (МПГ).

Прежде чем рассматривать метод, введем некоторые критерии, позволяющие достаточно объективно судить о сходстве или различии корреляционных векторов r₁, r₂, ..., r_n, дающих в совокупности матрицу коэффициентов корреляции Â размерностью n´n. Запишем любую пару сравниваемых векторов в развернутом виде: