Машиностроение \ Устройство и ремонт электрооборудования вагонов

Импульсный прерыватель (Расчетная часть дипломной работы), страница 3

Для лучшего восприятия найденных величин, выполним  следующее:

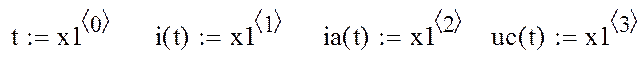
2.3.4 Результаты расчета

Таблица 2.5

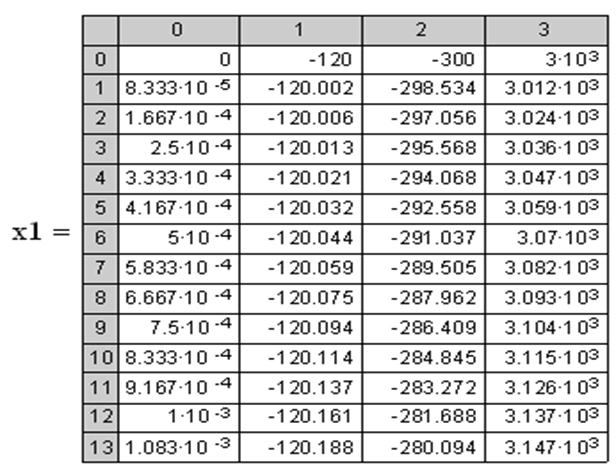
В таблице 2.5 приведено только 13 результатов расчета из 30000.

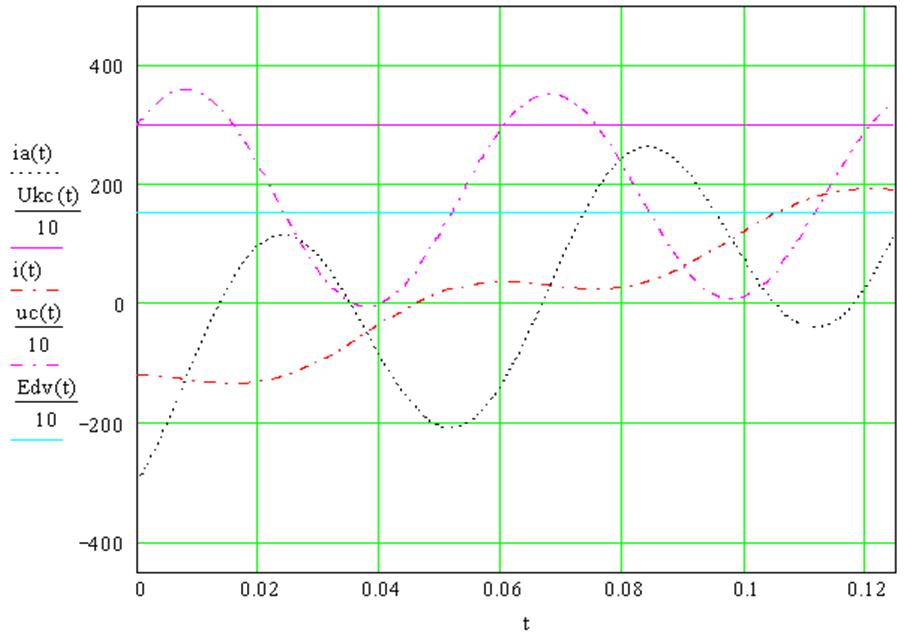
Рис. 2.12 Кривые решений системы дифференциальных уравнений.

Рис. 2.12 наглядно показывает, что при  невозможно без

импульсного управления получить тормозной эффект, двигатели автоматически переходят в тяговый режим. Весь расчет проведен при условии, что тиристор VS закрыт.

Приведенные выше рис. 2.10 ÷ 2.12 отражают процессы изменения параметров схемы при различных состояниях тиристора VS.Для получения картины изменения этих параметров при использовании импульсного регулирования, необходимо объединить выше описанные процессы.

2.3.5 Расчет параметров схемы при работе прерывателя с  

Для этого рассмотрим уравнения схемы:

1.  при открытом тиристоре

;

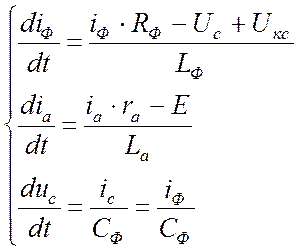2.  при закрытом состоянии

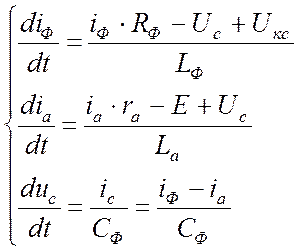
Как видно 2 система уравнений полностью содержит первую, и еще некоторые уравнения содержат дополнительные величины. Значит, если умножить эти величины на некоторую периодическую функцию, значения которой 0 или 1, то эта система, во времени, будет описывать оба состояния схемы.

Зададим эту функцию следующим образом:

      

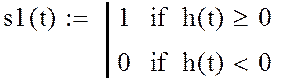
          где  частота работы тиристора.

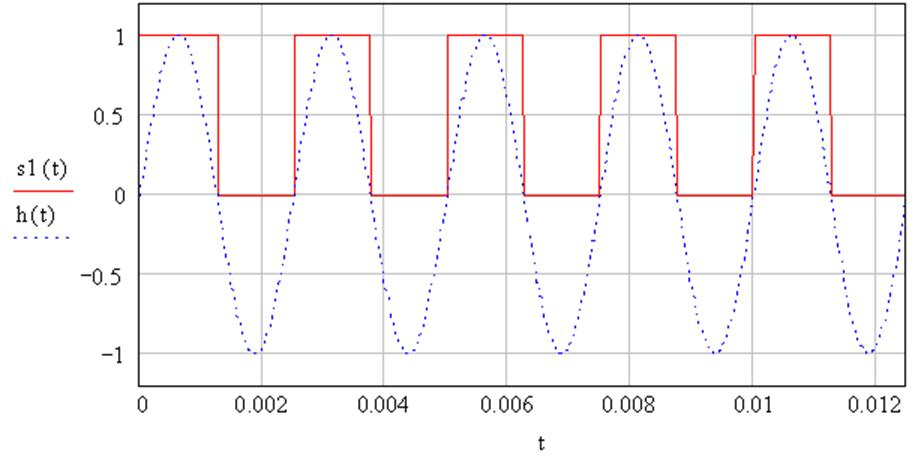
Рис. 2.13 Кривая изменения периодической функции.

Полученная таким образом функция, описывает работу прерывателя при коэффициенте заполнения импульсного цикла

 .

Тогда получим уравнения системы в следующем виде:

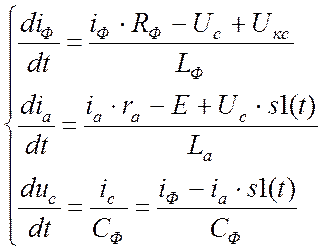
Рассчитаем эти уравнения.

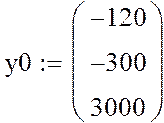
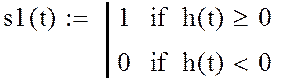
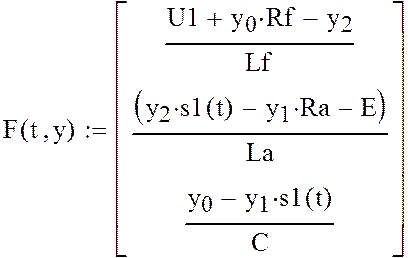
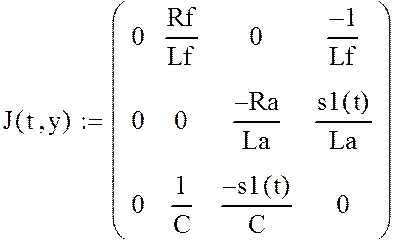
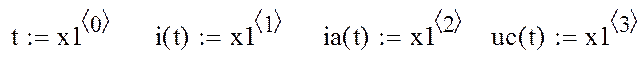
Результаты расчета приведены на рис. 2.14.

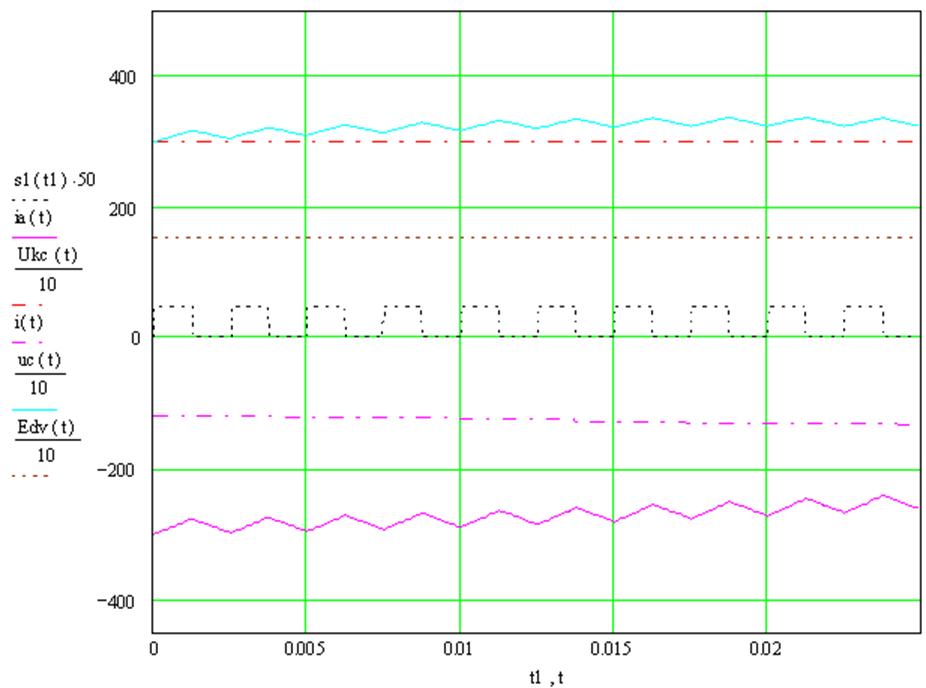
Рис. 2.14 Графики изменения токов и напряжения в режиме торможения.

Как видно из графика, при использовании импульсного прерывателя, режим торможения достигается даже при ЭДС < UКС.

Приведенный выше расчет сделан при работе импульсного прерывателя с коэффициентом заполнения импульсного цикла . Этот режим является наиболее тяжелым, т.к. пульсации тока торможения, как было показано выше, максимальны.

2.3.6 Расчет параметров схемы при работе прерывателя с  

Рассмотрим режим работы импульсного прерывателя с  . Для

моделирования этого режима необходимо изменить периодическую функцию

s1 (t) так, чтобы длительность состояния s1(t) = 1, была меньше полупериода работы тиристора. Этого можно достигнуть при помощи все той же синусоиды, но сместив ось аргумента на 0,5 вверх и подобрав соответствующий угол сдвига фазы. В результате проделанных операций получим функцию:

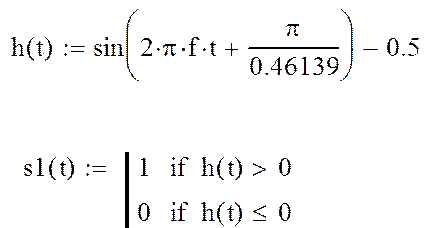
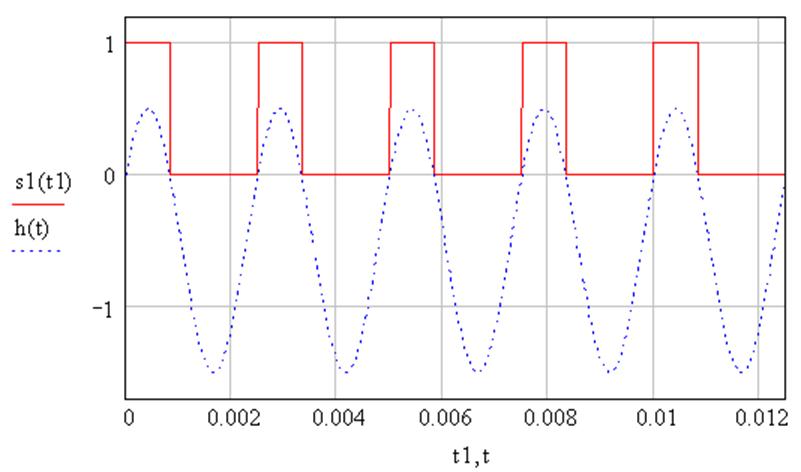
Рис. 2.15 График изменения периодической функции s1(t).

Расчет показывает, что в этом случае стабильный тормозной эффект достигается при . Это объясняется тем, что время закрытого состояния уменьшается, а, следовательно, время накопления энергии в увеличивается, что и обеспечивает постоянство тормозного тока.

Расчет проведен выше рассмотренным методом. Результаты отражены на рис. 2.16

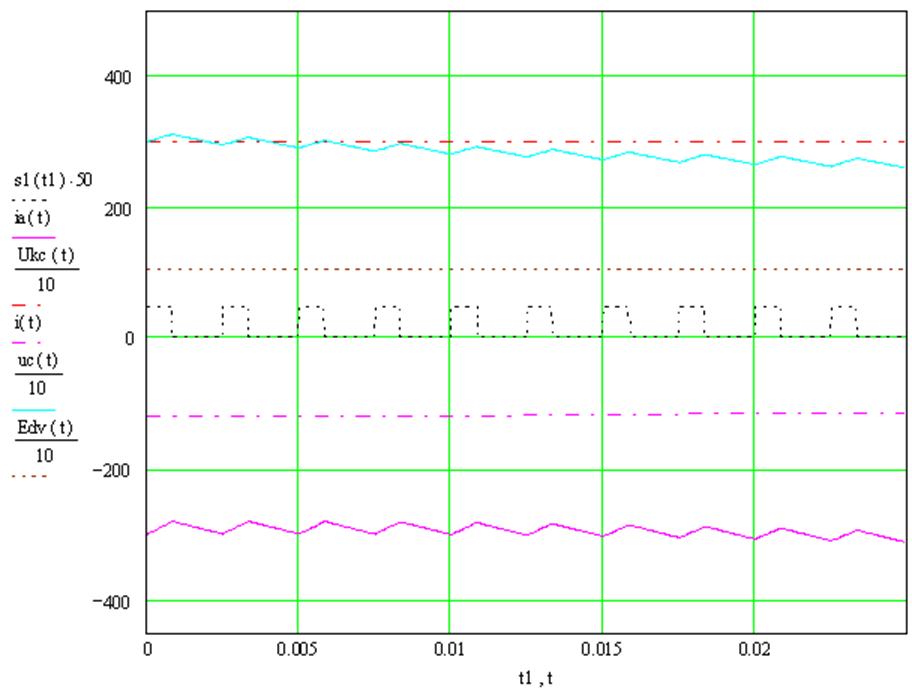
Рис. 2.16 График изменения токов и напряжения при .

2.3.7 Расчет параметров схемы при работе прерывателя с  

Рассмотрим режим работы прерывателя с , т.е. время открытого состояния тиристора < . Для обеспечения этого будем использовать следующую периодическую функцию:

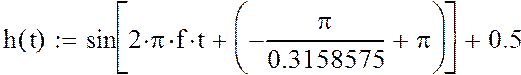
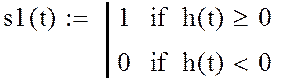
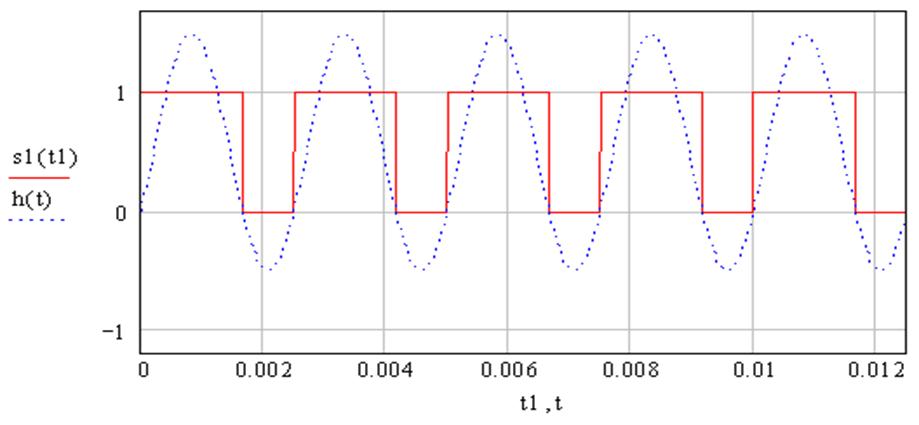
Рис. 2.17 График изменения периодической функции s1(t).

Как показывает расчет в этом режиме, для обеспечения устойчивого тормозного режима с постоянным током, необходимо иметь суммарную величину .Здесь, в отличие от предыдущего случая, время накопления энергии в  уменьшается, поэтому для обеспечения необходимой величины тормозного тока, требуется большее значение ЭДС.

Результаты расчета приведены на рис. 2.18.

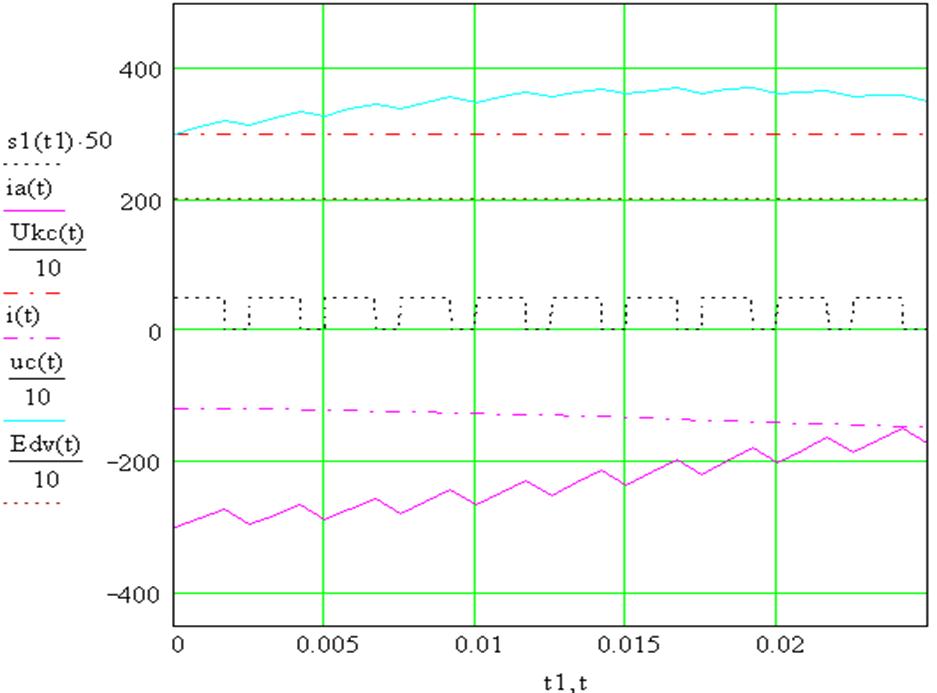
Рис. 2.18 График изменения токов и напряжения при .

2.3.8 Расчет параметров схемы при работе прерывателя с  

Рассмотрим режим рекуперации, когда . В этом случае импульсный прерыватель работает с , т. е. функция  s1(t) = 1 во всем интервале времени.

Как видно из графиков в этом случае процесс торможения проходит в установившемся режиме, поэтому никакого импульсного регулирования здесь не требуется. Этот процесс неуправляемый, поэтому невозможно добиться постоянства тормозного тока.

Результаты расчета приведены на рис. 2.19.

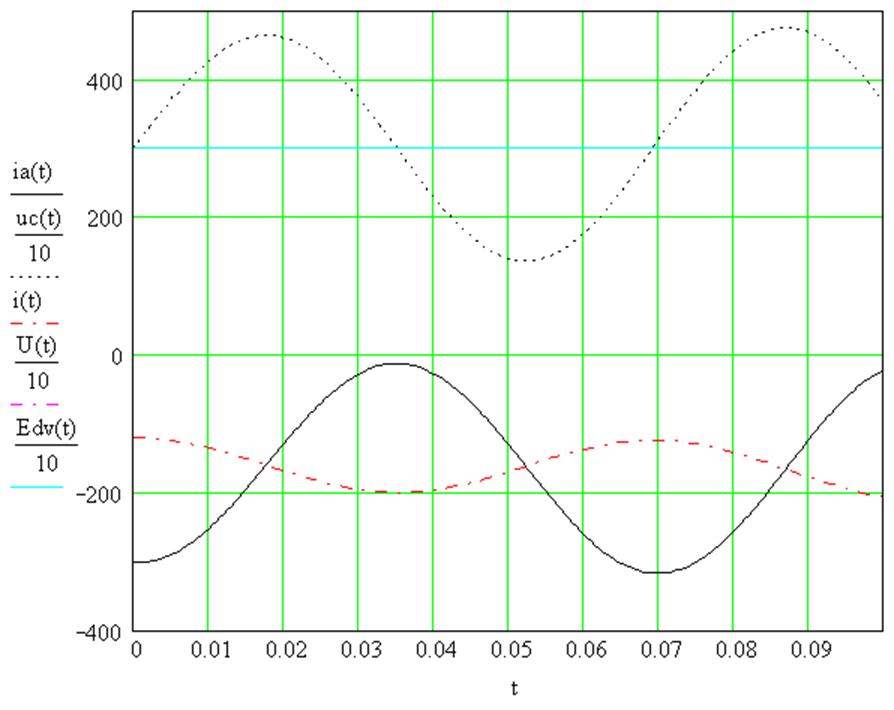
 Рис. 2.19 График изменения токов и напряжения при .

Расчет проведен с приведенными выше начальными условиями  и Е=3000 В.

2.3.9 Влияние величины ЭДС на процесс торможения

Все выше проведенные расчеты были сделаны при фиксированном  значении суммарной э. д. с. двигателей. Эти значения были подобраны в результате расчета уравнений для обеспечения установившегося режима торможения. Рассмотрим влияние величины ЭДС на процесс торможения. Для этого используем один из выше приведенных режимов работы прерывателя  при следующих условиях:

 , Е = var, начальные условия и методика расчета остаются прежними.

В качестве примера будем рассматривать режим с .Как было показано,  установившийся режим торможения достигается при  Е = 1050 В. (рис. 2.16).

1.  Вторым рассмотрим этот же режим, но при Е = 1000 В. (рис. 2.21)

2.  Е = 1100 В. (рис. 2.22)

Результаты расчета

Для удобства сравнения результатов расчета приведем сначала несколько измененный рис. 2.16.

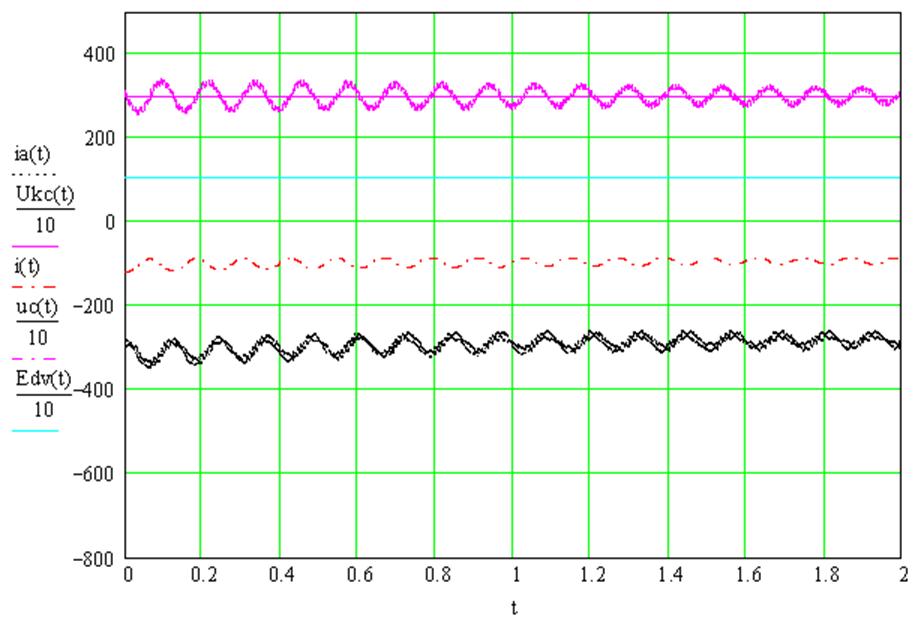
Рис. 2.20 Кривые изменения характеристик при  и Е = 1050 В.

1.

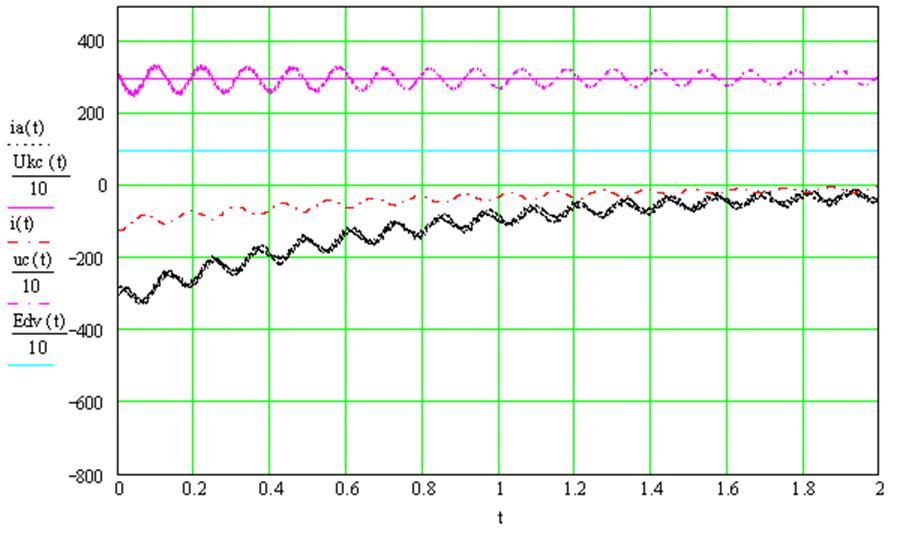
Рис. 2.21 Кривые изменения характеристик при  и Е = 1000 В.

2.

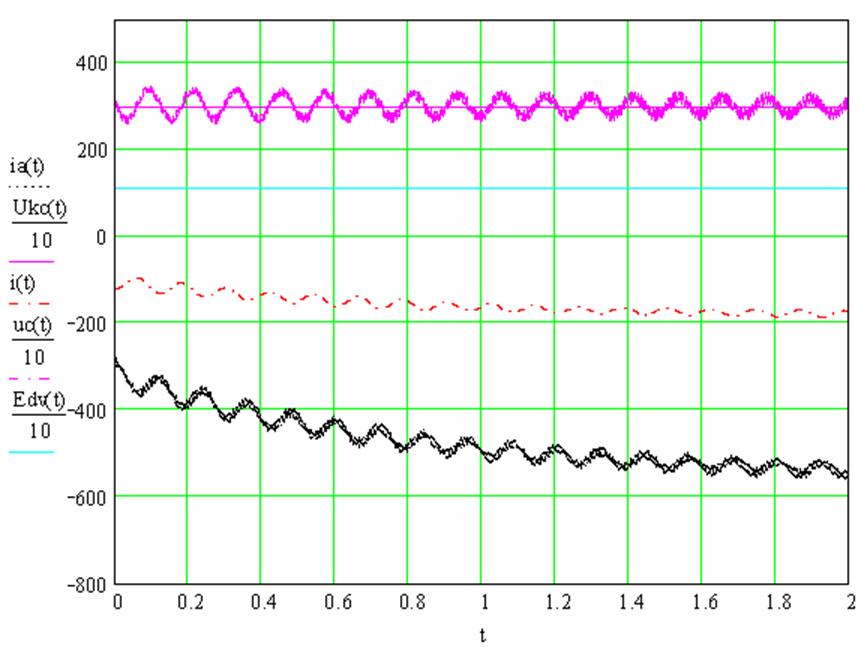
Рис. 2.22 Кривые изменения характеристик при  и Е = 1100 В.

Анализ показывает, что даже небольшое изменение величины ЭДС ведет к изменению тока цепи двигателей и тока рекуперации. Уменьшение ЭДС может привести к срыву торможения (рис. 2.21), а ее увеличение – изменению тока торможения выше допустимого значения (рис.2.22). Поэтому при использовании импульсного прерывателя для режима электрического торможения двигателей с независимым возбуждением, необходимо применять систему управления либо поддерживающую постоянство ЭДС, либо изменяющую величину γ в зависимости от изменения значения ЭДС.

Скачать файл