Машиностроение \ Устройство и ремонт электрооборудования вагонов

Импульсный прерыватель (Расчетная часть дипломной работы), страница 2

                        2.2 Расчет параметров входного фильтра.

2.2.1 Расчет емкости входного фильтра.

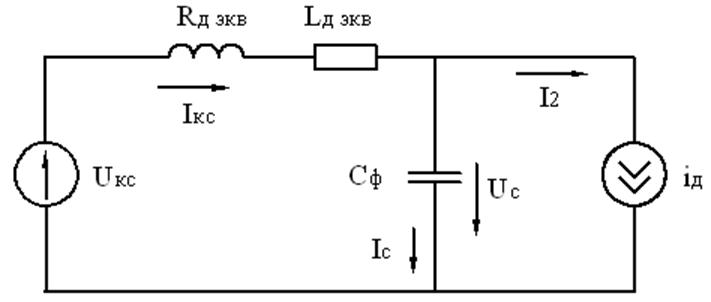
Подпись: Рис. 2.7 Схема замещения для цепи фильтра.
 


,

где   ток фильтра.

При открытом состоянии тиристора, ток .

Рассмотрим ток конденсатора.

Для диапазона времени       

                       

как видно на этом интервале ток емкости спадает.

При 

                   

в этом промежутке времени ток нарастает.

Модуль пульсации напряжения на конденсаторе:

                   

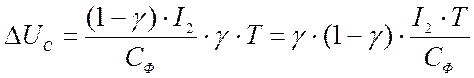
Значит, для того чтобы обеспечить необходимый уровень пульсации напряжения необходимо иметь емкость, удовлетворяющую следующему условию:

         

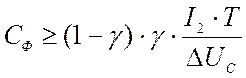
Расчет величины емкости фильтра проведем при следующих условиях:

          коэффициент заполнения импульсного цикла 

          допустимая величина пульсации ,

где относительная величина пульсации напряжения на входе прерывателя

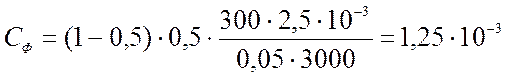            Ф

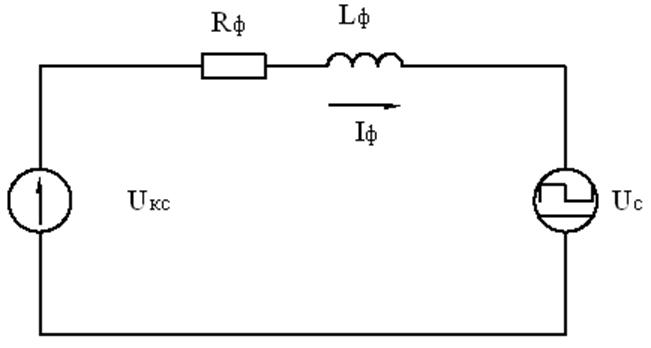
2.2.2 Расчет индуктивности входного фильтра.

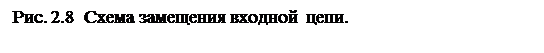Подпись: Рис. 2.8 Схема замещения входной цепи.
 


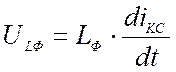
При малых приращениях Δt → 0 можно принять

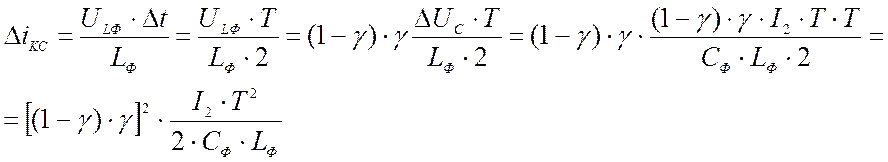
      Следовательно, для обеспечения требуемой величины пульсации, индуктивность входного фильтра должна удовлетворять следующему неравенству:

,

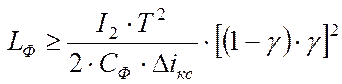          где величина пульсации тока на входе прерывателя;

                   

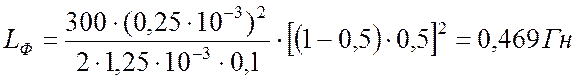
Результаты расчета сведем таблицу 2.4

Таблица 2.4

Наименование

Обозначение

Величина

Индуктивность входного фильтра

LФ

0,469 Гн

Емкость входного фильтра

СФ

 Ф

2.3 Моделирование процессов электрического торможения.

2.3.1 Принципиальная электрическая схема.

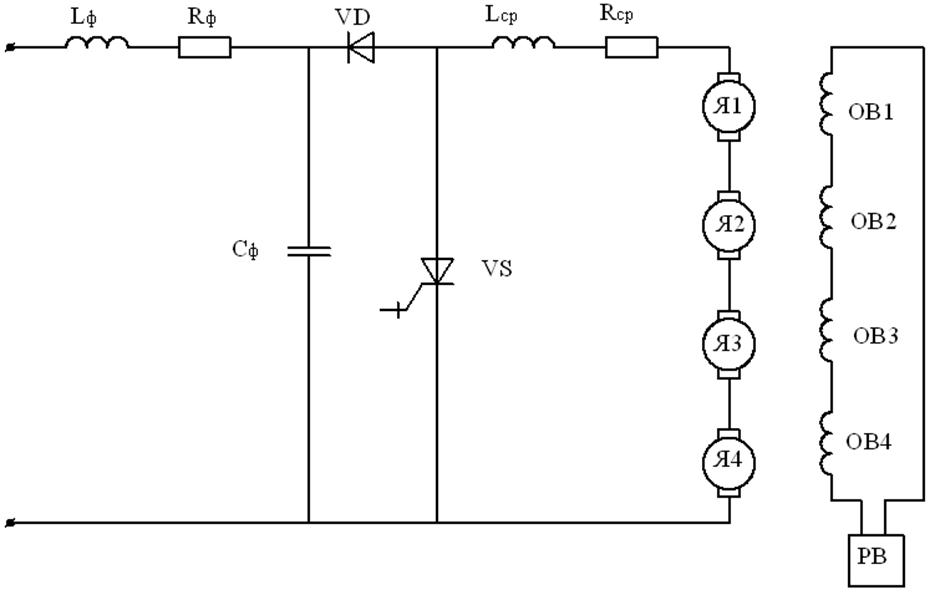
где РВ – регулятор возбуждения.

Процессы регулирования возбуждения в данном проекте не рассматриваются.

2.3.2 Составление уравнений описывающих процессы в преобразователе.

Процессы электрического торможения рассматриваем при следующих условиях:

        1. двигатели независимого возбуждения;

          2. конденсатор фильтра заряжен до напряжения контактной сети;

3. в цепи фильтра протекает ток рекуперации, т.е. установившийся режим;

4. сопротивление полупроводников в открытом состоянии 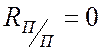 Ом, при закрытом .

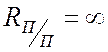Рассмотрим работу схемы в различные периоды времени.

Сначала рассмотрим интервал времени, когда тиристор VS открыт. Он разделяет схему на два независимых контура, один из которых содержит входной фильтр (рис. 2.9, а), другой цепь двигателей (рис.2.9, б).

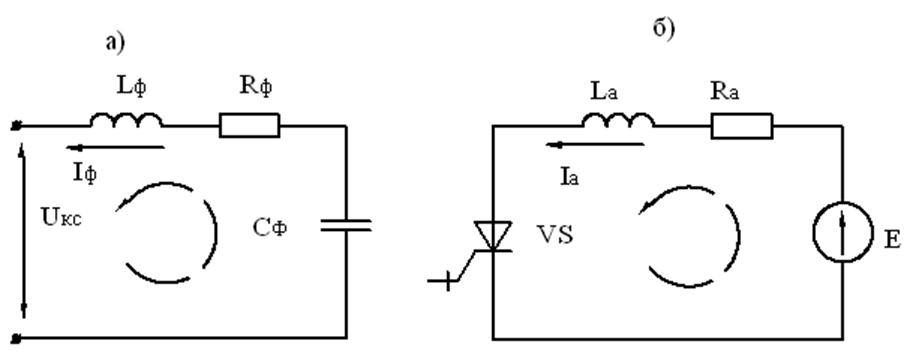
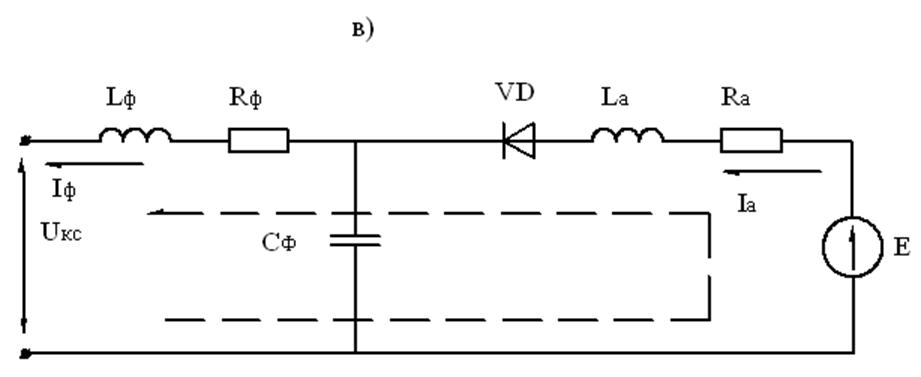
Рис. 2.9 Состояние схемы в различные периоды времени.

Цепь фильтра можно описать следующим уравнением:

,

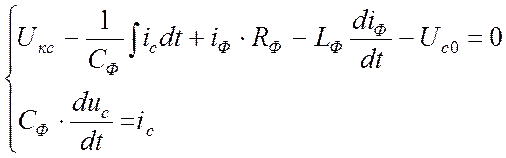где напряжение на конденсаторе в начальный момент времени.

Этот контур колебательный, поскольку содержит последовательно включенные  R, L и С, поэтому если процесс идет длительно, то ток фильтра будет изменяться во времени не только по величине, но и по направлению. Процесс изменения тока имеет периодический характер.

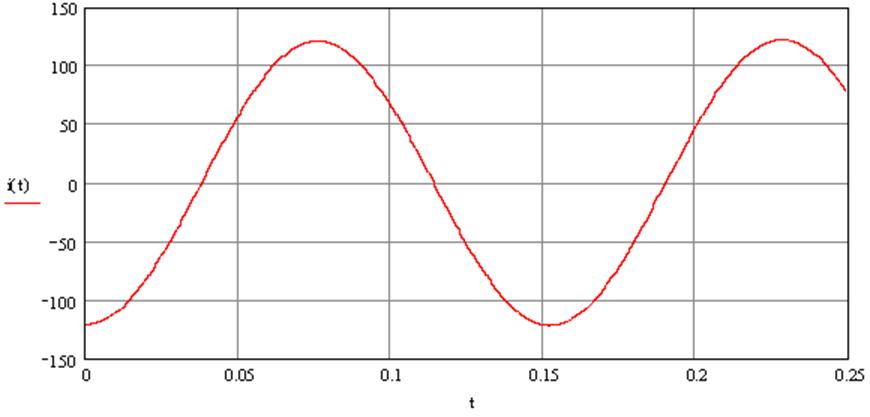
Рис. 2.10 Изменение тока фильтра.

На рис. 2.10 приведен процесс изменения тока фильтра после прекращения торможения – режим выбега.

Ток двигателей, а, следовательно, торможения, замыкается в цепи VS → La→ Ra.  Цепь двигателей описывается следующим уравнением:

         

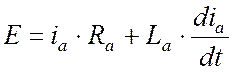
Индуктивность цепи накапливает энергию

          ,

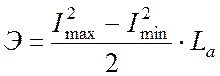где  суммарная индуктивность цепи якоря;

 максимальное и минимальное значение тока двигателя.

Эта энергия, в сумме с ЭДС двигателей, позволяет осуществить рекуперативное торможение при .

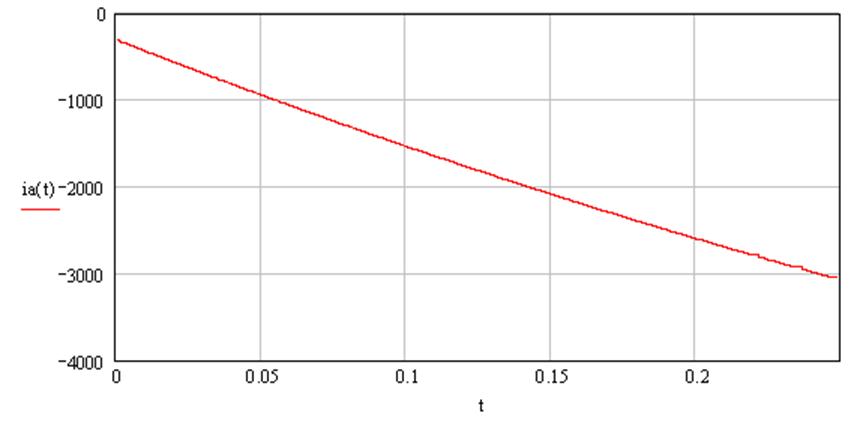
Рис. 2.11 Изменение тока двигателя.

Рис. 2.11. отражает характер изменения тока торможения, при  и постоянно открытом тиристоре VS.

Теперь рассмотрим схему при закрытом состоянии тиристора VS (рис. 2.9, в). Тогда  вся энергия, накопившаяся в La, прикладывается, через диод VD, к входному фильтру. При этом часть этой энергии тратится на заряд конденсатора, а часть уходит в контактную сеть в виде тока рекуперации.

В этом интервале схема представляет собой единое целое и поэтому не может быть описана двумя независимыми уравнениями. Составим систему

дифференциальных уравнений для этой цепи:

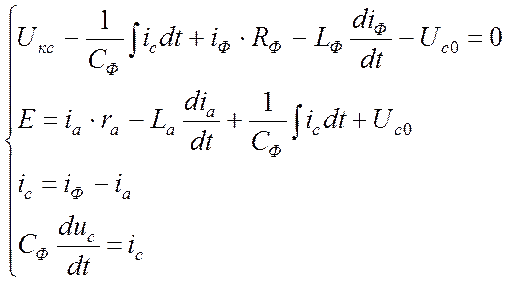
Для упрощения расчетов принимаем 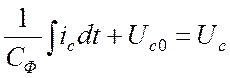      , тогда уравнения примут вид:

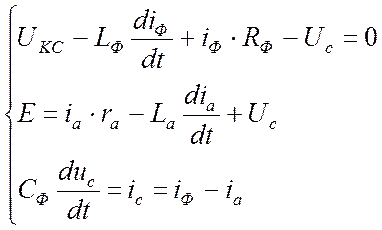
2. 3. 3 Решение дифференциальных уравнений

Выделим первые производные:

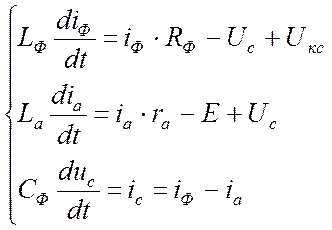
Решать эту систему дифференциальных уравнений будем с помощью встроенных функций MathCAD:

Stiffb (y0, t0, t1, M, F, J). Метод Булирша – Штера для жестких систем ОДУ.

Данная функция требует задания следующих параметров:

 вектор начальных условий, матрица, каждая строка которой содержит числовые значение искомой функции;

t0 – начальная точка переменной;

t1 – правая граница для интервала изменения переменной;

М – число шагов, которое должен использовать численный метод;

F – вектор-функция, каждая строка, которой содержит левую часть соответствующего уравнения системы.

J – матричная функция размерности N×(N+1), где N – число уравнений в системе. В первом столбце J должны находиться функции производных соответствующих строк F по t. В остальных N столбцах должен быть расположен якобиан (матрица частных производных всех функций для всех уравнений) решаемой системы дифференциальных уравнений.

Результатом работы функции Stiffb является матрица, в первом столбце которой содержатся значения переменной, а в остальных – соответствующие им величины искомых функций.

Применительно для нашего случая получим:

                              ,

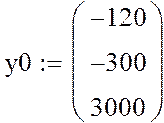где -120 – начальное значение тока фильтра – [А];

      -300 – начальное значение тока двигателя – [А];

       3000 - начальное значение напряжения на конденсаторе фильтра – [B].

                        – суммарная ЭДС двигателей.

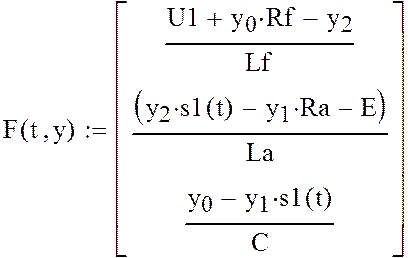
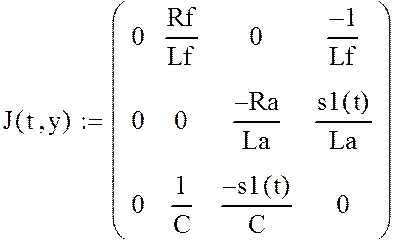
где х1 – матрица результатов расчета искомых функций, в первом столбце которой содержатся узловые величины переменной t, а в остальных – значения неизвестных функций системы, рассчитанные в этих точках. Порядок расположения столбцов с найденными величинами искомых функций определяется последовательностью, в которой они занесены в вектор у.

Скачать файл