Выбор оптимальных стратегий

Электронное

Пособие №4

Дисциплина АРМ и АЭС

Лабораторные и курсовые работы

Тема № 4: «Выбор оптимальных стратегий»

(Дополнительные варианты решения такого класса задач см. пособие по теме  №5)

Задание:

1.  Автоматизировать процесс определения дохода (выигрыша) применительно к задаче выбора моделей моечных машин;

2.  Автоматизировать процесс формирования матрицы выигрышей и выбора оптимальной стратегии по критерию «Оптимизация в среднем» и критерию Вальда.

Рекомендуемая литература:

1. М.М. Болотин. Автоматизированные рабочие места и экспертные системы вагоноремонтного производства. Учебное пособие (в двух книгах). МИИТ. 1996. – 109 с.
2. М.М. Болотин. Методические указания к лабораторным работам по дисциплине «Автоматизированные рабочие места и экспертные системы вагоноремонтного производства». МИИТ. 1997.- 38 с.
3. Джойс Нильсен. Microsoft Excel 97: справочник. –СПб: Питер Ком, 1999.-320 с.
4. Леонтьев Ю. Microsoft Office 2000: краткий курс. – СПб:Питер, 2001. – 288 с.
5. М.М. Болотин. Применение программ Excel и MathCAD в инженерных расчетах вагоноремонтного производства. Методические указания по выполнению  лабораторных и курсовых работ по дисциплине «Автоматизированные рабочие места и экспертные системы вагоноремонтного производства». МИИТ. 2005.

РЕКОМЕНДАЦИИ.

Классификация моделей поиска оптимальных стратегий

      Модели поиска оптимальных стратегий классифицируют по двум признакам [1. c. 41-49]:

·  По количеству критериев (многокритериальные и однокритериальные);

·  По наличию случайных и неопределенных факторов (модели принятия решений в условиях определенности, модели принятия решений в условиях риска и модели принятия решений в условиях стохастической неопределенности).

В качестве критериев для задач с полной определенностью принимают минимум удельных приведенных затрат, максимум прибыли или максимум индекса конкурентоспособности.

Для моделей принятия решений в условиях риска считается, что каждая стратегия может привести к одному из множества исходов, отличающихся вероятностью появления (вероятности появления ситуаций или событий считаются известными).

 Решение задач осуществляют в форме матрицы выигрышей или рисков (в строках первого столбца располагаются стратегии, а в следующих столбцах первой строки ситуации и вероятности их появления, в каждой клеточке матрицы на пересечении ой строки и го столбца записывается выигрыш или риск).

 В качестве критериев для матрицы выигрышей применяют «оптимизацию в среднем» 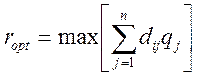 или принцип недостаточного основания Лапласа (вероятности всех событий полагаются одинаковыми)

,

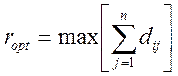где расчетный доход для стратегии и ой ситуации;

вероятность появления ой ситуации.

В качестве критерия для матрицы рисков принимается минимизация среднего риска .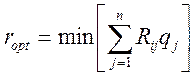

Под риском понимается разность между максимальным и текущим доходами для рассматриваемой ситуации:

.

В моделях принятия решений в условиях стохастической неопределенности (вероятности появления событий неизвестны) применяются специальные критерии:

критерий Вальда: ;

критерий Гурвица:  (коэффициент везучести      );

 критерий Сэвиджа: .

Для решения задач поиска оптимальных стратегий можно применить интегрированный пакет Microsoft Office/ Microsoft Excel.

Доход от реализации любого вида продукции (услуг) применительно к вагоноремонтному производству можно приближенно определять по формуле:

 ,

где Ц – стоимость ремонтной продукции, руб./шт.;

 N – возможный спрос на продукцию (объем выпуска продукции);

 себестоимость годового объема выпуска продукции машинами;                                (1)

себестоимость годового выпуска продукции участком;                                                (2)

затраты на материалы и запасные части для ремонта единицы продукции, руб./шт.;

затраты на жидкость при обмывке одного объекта, руб./шт.;

стоимость моющей жидкости, руб./м³;

расход моющей жидкости машиной, м³/ч;

Q_ф – фактическая производительность машины (объекта), шт./ч;

необходимое количество машин, шт.;

Ф – номинальный годовой фонд времени работы машины (объекта), час;

Р_у – установленная мощность электродвигателей оборудования, КВт;

q – количество рабочих в смену (количество рабочих, обслуживающих одну машину), чел.;

w – площадь производственного участка (машины), м²;

С_о – стоимость оборудования, размещенного на участке (стоимость машины), руб.

Постановка задачи оптимального выбора моечной машины для обмывки тележек по критерию «Оптимизация в среднем» и критерию Вальда.

На рынке предлагаются три модели моечных машин, отличающихся производительностью (это стратегии). Предполагаем, что спрос на процессы обмывки тележек может быть пониженным(N=25000, Ц=0,47 руб./шт.), средним (N=40000, Ц=0,51 руб./шт.) и повышенным (N=50000, Ц=0,71 руб./шт.) - это ситуации, отличающиеся объемом спроса и вероятностью их появления. Расчет себестоимости осуществляем по формуле (1).

Технология решения задачи

·  Вставка. Объект. Лист Microsoft Excel.

·  Вводим исходные данные, характеризующие параметры анализируемых моечных машин (или других объектов, процессов) и ситуацию №1, а также формулы для расчета себестоимости и дохода.

Программа расчетов дохода, формирования матрицы выигрышей

и выбора оптимальной стратегии.

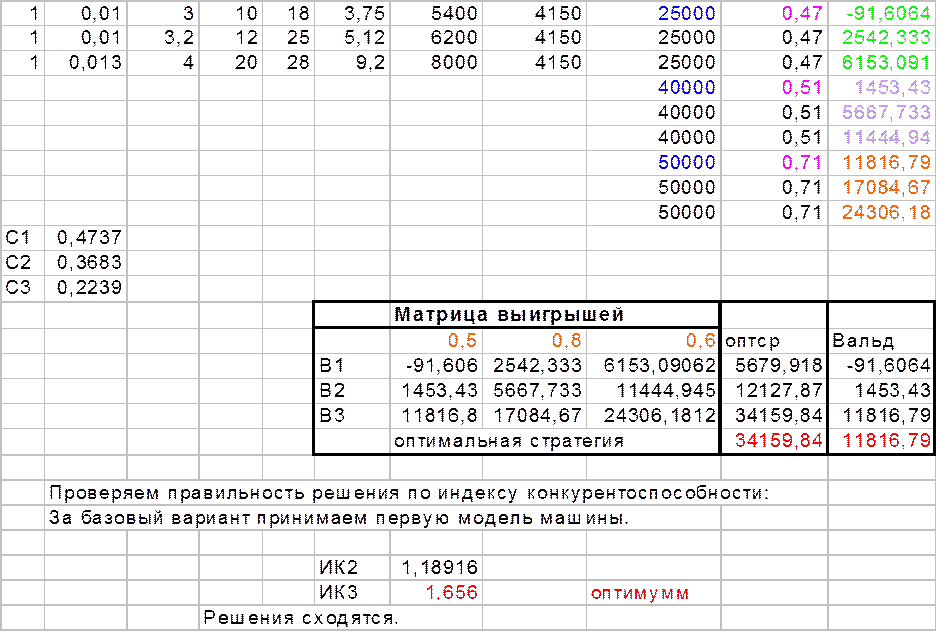
Для постановки задач по выбору оптимальных стратегий применительно к индивидуальным заданиям можно руководствоваться рассмотренным примером и примерами решения аналогичных задач, приведенными  в работах  [1, c.47-49; 2, с. 27-29].

Справочные данные:

Характеристики моечных машин для обмывки колесных пар и деталей вагонов (цены условные):

Показатели	Машина для колесных пар	Машина для деталей
Qф, шт./час	5,5	2(кассеты)
Py, кВт	21	11,2
Qв,	90	14
W,	6,2	9
Цв,	0,01	0,01
Со, руб.	9000	5000