Hs-диаграмма адиабатного истечения. Расход рабочего тела. Зависимость расхода от степени расширения газа

Для идеального газа (1.62) принимает следующий вид, если учесть, что h =с_рТ, с_р= kR/(k - 1)  и   pv = RT:

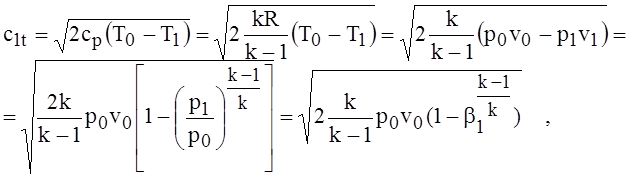      (1.63)

где 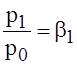    - отношение давлений в сопловом канале.

     Во всех приведенных формулах давление р следует подставить в Па, удельный объем v– в м³ /кг, энтальпии h - в Дж/кг, скорость с – в м/c.

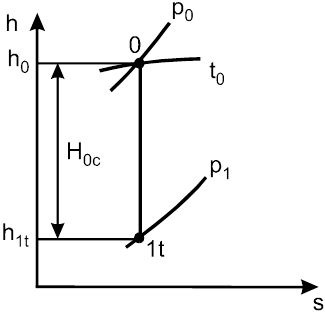Рис. 1.21. hs-диаграмма адиабатного истечения

При расчете с_1t по формулам (1.63) неизвестные параметры находятся из уравнения адиабаты  Показатель адиабаты k принимают равным: k = 1,4 для газов; k = 1,29 для перегретого водяного пара; k =1,035+0,1x для влажного водяного пара; k = 1,135 для сухого водяного пара.

Располагаемый теплоперепад сопла H_0с=h₀ – h_1t можно просто определить, используя соответствующую hs-диаграмму (рис. 1.21).

1.10.1.Расход рабочего тела

Важной характеристикой потока является расход рабочего тела через сопло. Условием неразрывности течения в потоке заключается в одинаковости массового расхода рабочего тела в любом сечении

.                                        (1.64)

Здесь для рассматриваемого сечения: G - расход рабочего тела, кг/с;

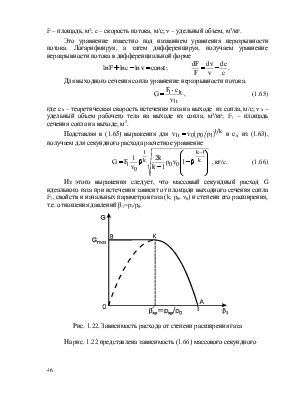
F – площадь, м²; c – скорость потока, м/с; v – удельный объем, м³/кг.

Это уравнение известно под названием уравнения неразрывности потока. Логарифмируя, а затем дифференцируя, получаем уравнение неразрывности потока в дифференциальной форме

;              .

Для выходного сечения сопла уравнение неразрывности потока.

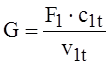,                                        (1.65)

где с_1t – теоретическая скорость истечения газа на выходе  из сопла, м/с; v_1t – удельный объем рабочего тела на выходе из сопла, м³/кг; F₁ – площадь сечения сопла на выходе, м².

Подставляя в (1.65) выражения для  и с_1t из (1.63), получаем для секундного расхода расчетное уравнение

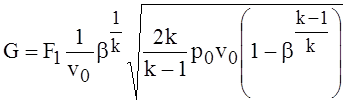 , кг/c.               (1.66)

Из этого выражения следует, что массовый секундный расход G идеального газа при истечении зависит от площади выходного сечения сопла F₁, свойств и начальных параметров газа (k, р₀, v₀) и степени его расширения, т.е. отношения давлений β₁=р₁/р₀.

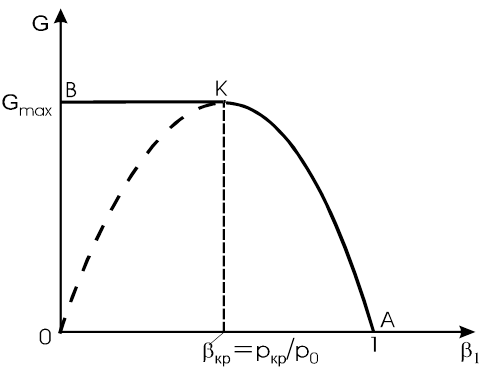Рис. 1.22. Зависимость расхода от степени расширения газа

На рис. 1.22 представлена зависимость (1.66) массового секундного расхода G от b₁ - кривая 0-К-А. При р₁ = р₀  (b₁=1) в точке А расход G = 0. При уменьшении давления среды р₁ за соплом (b₁ <1) расход газа растет и достигает максимального значения при так называемом критическом отношении давлений р_кр/р₀ =. При дальнейшем уменьшении р₁ расход падает, и для β₁ = 0 становится равным нулю.

Как показывает анализ функции G(β₁) на экстремум, значение β_кр , при котором достигается максимум расхода G_max , равно:

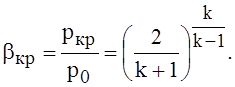                                     (1.67)

Из (1.67) следует, что  зависит только от показателя адиабаты k, т.е. от природы рабочего тела: для одноатомных газов (k=1.67) = 0,487; для двухатомных газов (k=1.4) = 0,528; для трехатомных газов и перегретого пара (k=1.29) =0,546; для сухого насыщенного пара (k=1.135) =0,577.

Подставляя в (1.66) значение , получаем

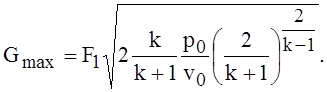
Экспериментально подтверждается только часть АК теоретической кривой, приведенной на рис.1.22. Вместо ниспадающей ветви К0 эксперименты при 0< β₁ <дают прямую постоянного расхода КВ, т. е. при достижении максимального значения  расход остается постоянным при снижении давления за соплом р₁ ниже критического значения р_кр.

Постоянство расхода при β₁ <объясняется тем, что невозможно получить давление газа на срезе суживающегося сопла ниже некоторого значения, называемого критическим,

 p_кр=β_кр ×p₀=const,                                   (1.68)

как бы мы ни понижали давление p₁ внешней среды, куда происходит истечение. Следовательно, p_кр есть наименьшее давление в устье суживающегося сопла.

1.10.2.Критический режим истечения

Соответствующая критическому давлению p_кр скорость с_кр на выходе из сопла также называется критической, и формулу для нее можно получить из (1.63) после подстановки β_кр, а также параметров состояния  (из уравнения адиабаты) и  :

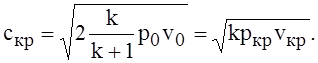                           (1.69)

Выражение (1.69) совпадает с известной из физики формулой для скорости звука а, и, следовательно, с_кр= а = const при заданных локальных значениях критических параметров p_кр, v_кр и показателя адиабаты k, характеризующего природу газа.

Скорость звука есть скорость распространения в среде малых возмущений, поэтому критическая скорость истечения газа с_кр является максимальной скоростью на выходе из суживающегося сопла. В критическом режиме истечения никакое упругое возмущение, например, уменьшение давления внешней среды p₁, не передается внутрь сопла—оно просто сносится потоком истекающего газа, движущимся с той же скоростью, с какой распространяются упругие внешние возмущения p₁. Поэтому в случае критического истечения в сопле не происходит перераспределения давления.