Hs-диаграмма адиабатного истечения. Расход рабочего тела. Зависимость расхода от степени расширения газа, страница 2

Критическая скорость может быть также определена формуле:

 , м/с.                             (1.70)

1.10.3.Адиабатное течение в канале переменного сечения

Рассмотрим в общем случае поведение параметров при течении идеального газа по длине канала переменного сечения без теплообмена с окружающей средой (адиабатный процесс). Запишем следующую систему уравнений в дифференциальной форме:

уравнение неразрывности   (Fс/v = const)

dF/F = dv/v — dс/с;                              (1.71)

уравнение адиабаты   (pv^k = const)

dv/v=-(1/k)dp/p;                                   (1.72)

уравнение энергии адиабатного течения

сdс = -vdp.                                           (1.73)

Совместным решением уравнений (1.71 - 1.73), получаем

 .                                      (1.74)

В этом уравнении отношение скорости течения потока с к скорости звука a называется числом Маха:

.

Уравнение (1.74) связывает между собой изменение площади сечения канала с изменением скорости потока в зависимости от соотношения между скоростью звука и скоростью потока. Основываясь на этом уравнении, проведем анализ указанных зависимостей. Увеличение скорости потока газа происходит за счет падения давления, т. е. dс > 0 при dp < 0, при этом могут иметь место следующие случаи.

Случай 1. c < а, М < 1; течение— докритическое, поскольку скорость потока имеет значение ниже местной скорости звука. В этом случае из (1.74) следует, что dF < 0, т. е. сопло по течению потока должно сужаться.

Случай 2. с=a, М=1; течение— критическое: с=с_кр=а. В соответствии с (1.74) этот случай реализуется при dF = 0, т. е. в самом узком сечении сопла, которое носит название критического F_min=F_кр.

Случай 3. с > а, М > 1; течение— сверхкритическое, так как с> а). Здесь по (1.74) dF > 0, что означает увеличение сечения сопла вдоль потока, т.е. сопло должно расширяться.

Приведенный анализ показывает, какой профиль должно иметь сопло, чтобы поток имел на выходе сверхзвуковую скорость. Давление за соплом должно быть меньше критического: р₁ < р_1кр (p₁/p₀ < β_кр). Сопло в этом случае необходимо составить из двух частей - суживающейся (для достижения критических параметров: р_кр и с_кр= а) и расширяющейся, где с > а (рис.1.23).

1.10.4.Сопло Лаваля

Комбинированное сопло состоящее из двух частей - суживающейся и расширяющейся, называется соплом Лаваля, по имени шведского инженера, первым применившего его для получения сверхзвуковых скоростей пара.

При конструировании сопел Лаваля учитывается то отбстоятельство, что при углах конусности расширяющейся части сопла, превышающих 10—12°, происходит отрыв струи от стенок канала. Это приводит к необратимым потерям энергии на вихреобразование и исключает дальнейшее увеличение скорости потока выше скорости звука.

Рис. 1.23. Профиль сопла Лаваля и графики изменения давления и скоростей

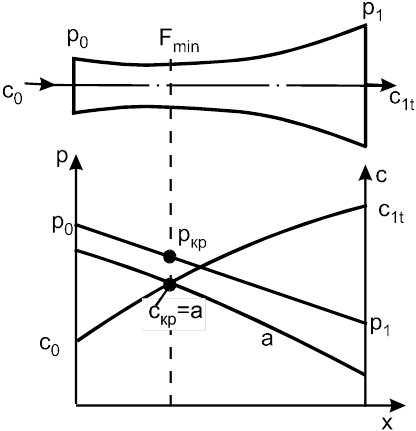х – направление оси сопла

При известном значении максимального расхода газа через сопло площадь минимального сечения F_min определяется по уравнению неразрывности потока

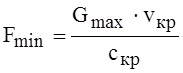, м².

Если заданное значение давления на выходе из сопла р₁ больше р_кр, выбирают простое суживающееся сопло, если меньше – сопло Лаваля.

При истечении водяного пара все общие законы, установленные для истечения газов, остаются  в силе. Однако формулы истечения, в которые входит  величина k, для водяного пара будут приближенными, так как значение k для пара в процессе изменения его состояния непостоянно.

Рассмотрим теперь движение газа через другой тип каналов – диффузор. Диффузор - канал, предназначенный для увеличения давления газа за счет уменьшения его скорости, т.е. в диффузоре dp > 0, dc <0. Из уравнения (1.74) следует, что если М<1, то dF>0, т.е. если скорость газа при входе в канал меньше скорости звука, то площадь сечения диффузора должна увеличиваться по направлению движения газа. Если же скорость газа на входе  в канал больше скорости звука (с>a, М>1). то диффузор должен суживаться. Таким образом, форма диффузора тоже может быть, как и форма сопла, суживающейся или расширяющейся.

1.10.5. Истечение с трением

Действительная скорость истечения с₁ из-за потерь трения оказывается меньше теоретической с_1t, определяемой формулами (1.62), (1.60). Поэтому в инженерной практике используется эмпирическая поправка на трение j, называемая скоростным коэффициентом сопла. Действительная скорость истечения определяется по формуле

c₁ = j×c_1t.                                                (1.75)

Потеря кинетической энергии в действительном процессе

Dh_c =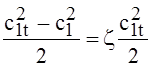  Дж/кг.

Здесь коэффициент  z = 1 - j²  называется коэффициентом потерь энергии в сопле.