Задача 6–1.
Теплопередача при поперечном обтекании потоком жидкости или газа пакета труб, расположенных в шахматном порядке, характеризуется безразмерным числом Нуссельта.
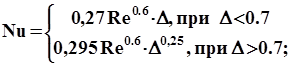 (1)
(1)
где 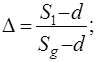 (2)
(2)
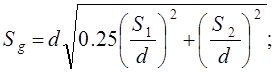 (3)
(3)
S1 – поперечный шаг рядов труб;
S2 – продольный шаг рядов труб;
Sg – диагональный шаг рядов труб;
d – диаметр труб.
Определить величину Nu и D при Re = 2×104, d = 25,4 мм, S1 = 60 мм и S2 = 30, 50, 65, 75, 80 мм.
|
134.09 |
2.03 |
|
….. |
….. |
|
….. |
….. |
|
102.79 |
0.57 |
Задача 6-2.
Интенсивность нестационарного массообмена химического вещества, находящегося в тигле, с атмосферой определяется по формуле:
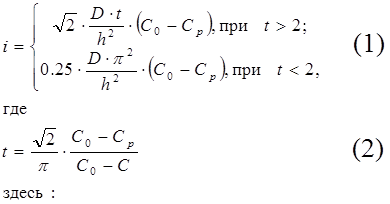
t – безразмерный параметр;
C – текущая концентрация вещества;
C0 – исходная концентрация вещества;
CP – равновесная концентрация вещества;
D – коэффициент диффузии вещества;
h – высота тигля.
Вычислить значения i и t при D = 6.3×10-5 см2/с, h = 2.5 см, C0 = 8.2%, CP = 1.7%, C = 8, 7.5, 7, 6, 4, 2 %.
|
0.001355 |
14.63014 |
|
….. |
….. |
|
….. |
….. |
|
0.000007 |
0.47194 |
Задача 6–3.
Для стальных и чугунных труб, уже находящихся в эксплуатации, коэффициент сопротивления определяется по формуле:
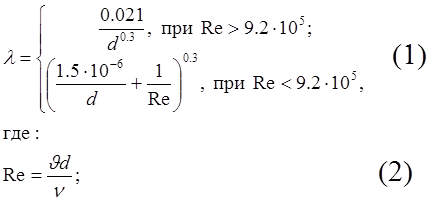
Re – число Рейнольдса (безразмерная величина);
d – диаметр трубы, см;
n – вязкость жидкости;
J – скорость жидкости.
Вычислить Re и l для течения воды (n = 0.009 см2/с) в трубе диаметром d = 19.1 мм со скоростью J = 1, 2, 5, 10, 20, 50, 100 м/с.
|
21222.2224 |
0.0505 |
|
….. |
….. |
|
….. |
….. |
|
2122222.2187 |
0.0172 |
Задача 6–4.
Величина продольного перемешивания в химической насадочной колонне характеризуется формулой:
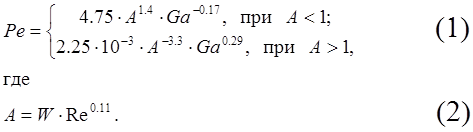
Здесь W, Pe, Re, Ga – безразмерный характеристики процесса (соответственно: безразмерная скорость, число Пекле, Рейнольдса, Галлилея).
Вычислить значения Pe и A при Ga = 0.9×105, Ra = 6.1×104, W = 0.1, 0.2, 0.5, 0.75, 0.85
|
0.1483 |
0.3360 |
|
….. |
….. |
|
….. |
….. |
|
0.0019 |
2.8563 |
Задача 6–5.
Конвективный теплообмен между горячим газом и пакетом вертикально расположенных труб водяного отопления характеризуется безразмерным числом Нуссельта, вычисляемым по формуле:
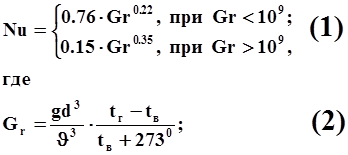
Gr – число Гросгофа (безразмерная величина);
d – диаметр труб;
J – вязкость газа;
g – ускорение силы тяжести;
tг – температура газа;
tв – температура воды;
Определить числа Gr и Nu при ![]() =
500°,
=
500°,
![]() =
15° и J =
=
15° и J = ![]() , d = 0.1, 0.2, 0.25, 0.275 и 0.3 м
, d = 0.1, 0.2, 0.25, 0.275 и 0.3 м
|
73423613.0 |
40.8 |
|
….. |
….. |
|
….. |
….. |
|
1982437552.0 |
269.2 |
Задача 6–6.
Динамическая удерживающая способность насадочной химической колонны характеризуется формулой:
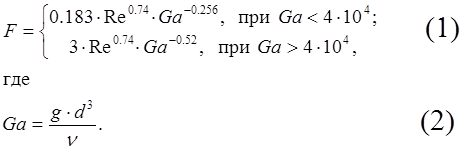
Здесь
Re – число Рейнольдса (безразмерная характеристика);
Ga – число Галлилея (безразмерная характеристика);
n – вязкость жидкости;
d – эквивалентный диаметр насадки;
g – ускорение силы тяжести.
Вычислить значения F и Ga при d = 2.5 см, Rе = 4.1×104 n = 0.01, 0.05, 0.1, 0.5, 1 и 2 см2/с.
|
0.01 |
1532810.0 |
4.7520 |
|
….. |
….. |
….. |
|
….. |
….. |
….. |
|
2.00 |
7664.05 |
48.0277 |
Задача 6–7.
Газожидкостная смесь движется по трубе диаметром d = 19.1 см со скоростью V. Коэффициент газонасыщенности смеси определяется по формуле:
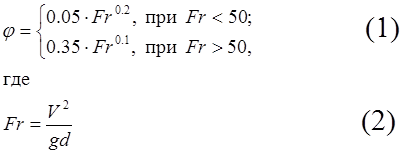
Здесь:
Fr – число Фрида (безразмерная величина);
g – ускорение силы тяжести.
Вычислить величину j и Fr при V = 1, 2, 5, 10, 20 и 50 м/с
|
0.044 |
0.533 |
|
….. |
….. |
|
….. |
….. |
|
0.718 |
1334.251 |
Задача 6–8.
Относительное количество жидкости, содержащееся в химической насадочной колонне, определяется формулой:
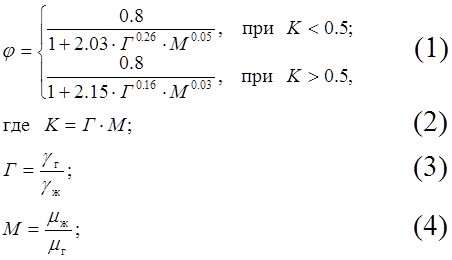
Здесь gг, gж – удельный вес газа и жидкости;
mг, mж – динамическая вязкость газа и жидкости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.