Теплопередача при поперечном обтекании потоком жидкости или газа пакета труб. Интенсивность нестационарного массообмена химического вещества, находящегося в тигле, страница 4

Определить  w  и  h¢  при  h = 15, 16, 17, 22, 23 см

82.495	-4.444
…..	…..
…..	…..
22.135	3.555

Задача 6–22.

Коэффициент сопротивления течению жидкости в шероховатых трубах определяется по формуле:

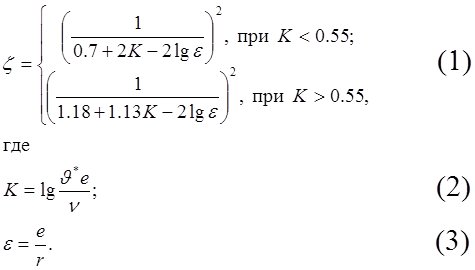
Здесь

J^* – динамическая скорость;

n   – вязкость жидкости;

e    – средняя высота выступов шероховатости;

e  – относительная шероховатость;

r     – радиус трубы.

Вычислить значения  z и  K  при  n = 0.009 см²/с,  e = 1 мм,  r = 15 см  и  J^* = 0.1, 0.2, 0.5, 1, 2 и 5 см/с.

0.0377	0.0457
…..	…..
0.0177	1.7447

Задача 6–23.

Газовый поток турбореактивного двигателя температурой  T₁ = 900K, давлением  P₁, молекулярным весом  M = 30 г/моль  и показателем адиабаты  k = 1.33  вытекает через сужающееся сопло в среду, имеющую давление  P₂ = 1 атм,  со скоростью

    

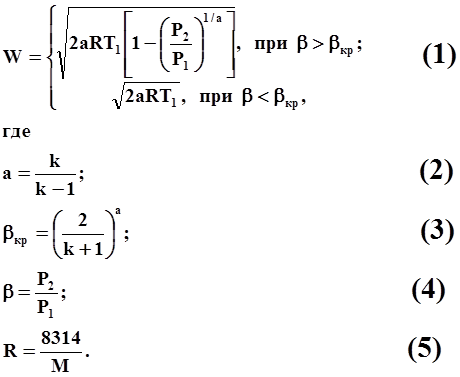
Здесь  R – газовая постоянная,  м²/с²×град.

Определить  b_кр, а также   W  и   b   при  P₁ = 1.4, 1.5, 1.6, 2.4, 2.5, 2.6 атм.

401.2860	0.7142
…..	…..
417.9127	0.3846

Задача 6–24.

При ламинарном течении жидкости в трубе теплообмен на входном и стабилизированном участках трубы характеризуется безразмерным числом Нуссельта:

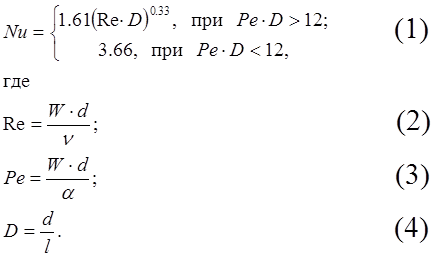
Здесь  Re  и  Pe  – безразмерные числа Рейнольдса и Пекле;

W,  n  – скорость движения и вязкость жидкости;

d,   l   – диаметр и длина трубы;

a  –  коэффициент температуро-проводимости.

Вычислить значения Pe×D и Nu  для течения воды с параметрами:  W = 0.3 м/с,  n = 9.5×10^-3 см²/с,  d = 18 мм, a = 3×10^-3 см²/с,   l = 5, 10, 20, 50, 100 м.

64.799	4.359
…..	…..
…..	…..
3.239	3.659

Задача 6–25.

Скорость химической реакции в диффузионном и кинетическом режиме определяется уравнением:

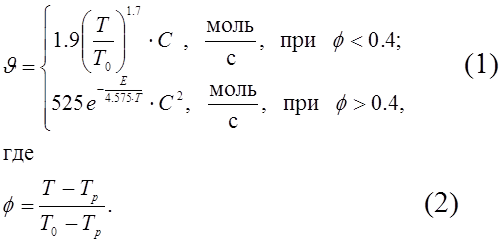
Здесь   T,  T₀, T_P  – текущая, исходная и равновесная температуры процесса;

f  – безразмерная температура процесса;

E    – энергия активации реакции.

Вычислить  f  и  J  при  E = 16700 кал/моль,  C = 0.96 моль/см³, T₀ = 290 K,   T_P = 1530 K,   T = 800, 900, 1000, 1050, 1080 K.

0.588	5.042
…..	…..
…..	…..
0.362	17.051

Задача 6–26.

Теплопередача при поперечном обтекании воздухом одиночного цилиндра определяется уравнением:

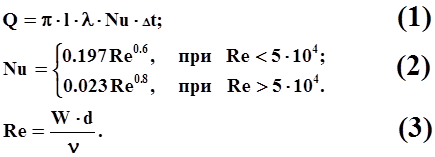
Здесь  Nu, Re  – безразмерные числа Нуссельта и Рейнольдса;

l  – коэффициент теплопроводности цилиндра;

d, l  – диаметр и длина цилиндра;

W, n – скорость и вязкость воздушного потока;

Dt – температурный перепад.

Вычислить значения Q,  Nu иRe при  d = 25 см, l = 6 м, n = 2.2×10^-5 м²/с,   Dt = 80°,    l = 8.3×10^-6 ккал/м×с×град,   W = 1, 2, 5, 10, 20 м/с.

0.66	53.42	11363.63
…..	…..	…..
…..	…..	…..
5.55	443.57	227272.72

Задача 6–27.

Гладкая плита длиной  l = 150 см  обдувается потоком воздуха со скоростью  W.  Теплообмен плиты с воздухом характеризуется коэффициентом:

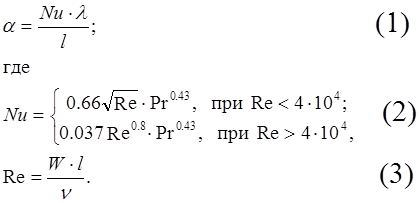
Здесь  Nu,  Pr   и  Re  – безразмерные числа Нуссельта, Прандтля и Рейнольдса;

l = 0.026 вт/м×град  – теплопроводность плиты;

n = 1.43×10^-5 м²/с     –  вязкость воздуха;

Вычислить значения  a,  Nu  и  Re,  если Pr = 0.7,  W = 0.1, 0.2, 0.5, 1, 2, 5 м/с.

1.00	57.98	10489.51
…..	…..	…..
…..	…..	…..
20.71	1195.01	524475.52

Задача 6–28.

При обтекании твердой сферы жидкостью, коэффициент лобового сопротивления сферы рассчитывают по формуле:

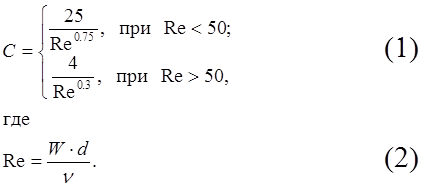
Здесь Re – безразмерное число Рейнольдса;

W, n – скорость и вязкость жидкости;

d – диаметр сферы.

Определить значения  C  и  Re  при   d = 3 мм,   n = 0.014 см²/с  и  W = 1, 2, 5, 7, 10 см/с.

2.5101	21.4285
…..	…..
…..	…..
0.7993	214.2857