Теплопередача при поперечном обтекании потоком жидкости или газа пакета труб. Интенсивность нестационарного массообмена химического вещества, находящегося в тигле, страница 3

421.599	-0.171	0.000
…..	…..	…..
…..	…..	…..
502.076	1.122	1.029

Задача 6–16.

По вертикальной трубе квадратного сечения шириной  a = 4 см, длиной  l = 3 м, теплопроводностью  l = 0.032 ккал/м×ч×град  и температурой стенок  t_c = 30°С двигается горячий воздух вязкостью n = 2.3×10^-5 м²/с,  температурой  t_в = 150°С  и скоростью  W.   Теплоотдача от воздуха к трубе определяется формулой:

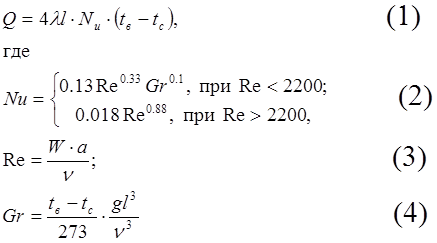
Здесь  Nu,  Re,  Gr  – безразмерные числа Нуссельта, Рейнольдса и Грасгофа.

Определить значения  Re,  Nu  и  Q  при  W = 0.5, 1, 2, 5, 10 м/с.

869.565	16.524	761.448
…..	…..	…..
…..	…..	…..
17391.304	96.998	4469.688

Задача 6–17.

Массивный бак, заполненный водой до уровня  h₁ = 5 м соединён на высоте  h = 1 м от дна трубой диаметром  d₁ = 3.5 см с малым переливным баком. Малый бак содержит донное отверстие диаметром d₁. Определить высоту жидкости в малом баке:

   

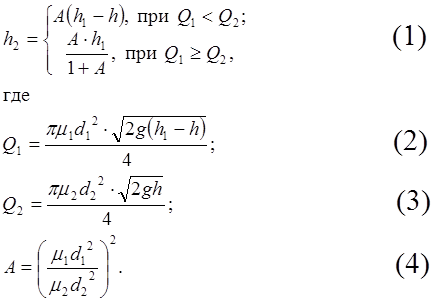
Здесь  m₁,  Q₁   – коэффициент расхода и расход воды через переливную трубу;

m₂,  Q₂   – коэффициент расхода и расход воды через донное отверстие;

g – ускорение силы тяжести.

Вычислить  , Q₁  и  Q₂  при  m₁ = 0.9,  m₂ = 0.6  и  d₂ = 3, 5, 7, 10 и 15 см.

403.25	7667.01	1877.63
…..	…..	…..
…..	…..	…..
2.66	7667.01	46940.92

Задача 6–18.

При турбулентном течении жидкости в трубах с гладкими стенками коэффициент сопротивления определяется по формуле

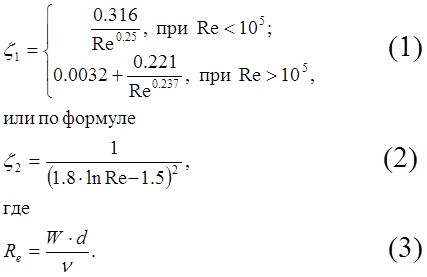
Здесь  Re – число Рейнольдса;

W,  n  – скорость течения и вязкость жидкости;

d  – диаметр трубы.

Определить значения  z₁,  z₂  и  Re при  d = 35 см,  n = 0.026 см²/с  и  W = 0.1, 0.2, 0.5, 1, 2 и 5 м/с.

0.0293	0.0284	13461.5384
…..	…..	…..
…..	…..	…..
0.0123	0.0123	673076.9218

Задача 6–19.

Концентрация вещества, возникающего в результате химической реакции второго порядка (коэффициент скорости  k₂ ), осложнённой побочными реакциями первого и нулевого порядка (коэффициенты сккорости  k₁  и  k₀ ), определяется уравнением:

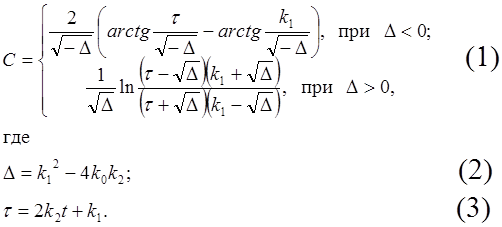
Вычислить значения  C  и   D  для времени процесса  t = 15 c  и  следующих констант:

¹	k0	k1	k2
1	5.1	6.9	1.2
2	2.7	6.1	4.3
3	5.4	-3.8	1.5
4	2.1	3.3	4.3
5	-7.7	8.5	-1.2

0.311	23.180
…..	…..
…..	…..
0.365	35.289

Задача 6–20.

Теплообмен жидкости при свободной конвекции характеризуется безразмерным числом Нуссельта согласно уравнению:

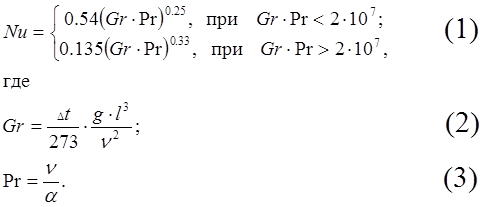
Здесь  Gr  и  Pr – безразмерные числа Грасгофа и Прандтля.

Dt – температурный перепад;

g – ускорение силы тяжести;

l – толщина слоя жидкости;

n, a – коэффициенты вязкости и температуропроводности жидкости.

Вычислить значения Gr×Pr   и   Nu  при охлаждении трансформаторного масла с параметрами: Dt = 40°,  l = 15 см,  a = 3.5×10^-3 см²/с,  n = 1, 2, 5, 7, 10 см²/с.

138461540.00	65.61	(18.53)
…..	…..	…..
…..	…..	…..
13846153.87	32.94	(10.42)

Задача 6–21.

Цилиндрический сосуд с внутренним диаметром d₁ = 18 см  и высотой  l = 25 см,  закрыт крышкой, имеющей в центре отверстие диаметром  d₂ = 12 см, заполнен до высоты   h  жидкостью и приведён во вращение относительно оси. Угловая скорость вращения, при которой жидкость начинает выплёскиваться через отверстие, определяется по формуле:

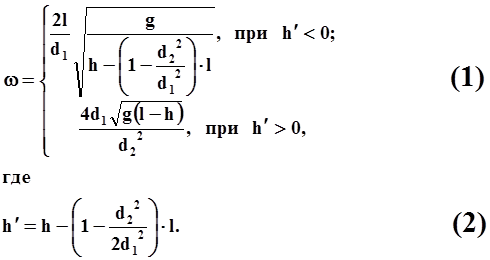
Здесь  g – ускорение силы тяжести.