220400 Математический анализ Толстиков А.В.
Курс 1. Семестр 1. Лекция 4. Комплексные числа
План
1. Комплексные числа. Поле комплексных чисел. Комплексно-сопряженные числа. 2. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа. Тригонометрические формы комплексного числа. 3. Корни из комплексных чисел. 4. Показательная форма комплексного числа. Формула Эйлера.
Литература: Ильин В.А., с.196-200. Письменный Д., с. 186-192.
§ 1. Комплексные числа. Поле комплексных чисел. Комплексно-сопряженные числа
Определение 1.1. Комплексным числом z называется упорядоченная пара действительных чисел(x, y).
Обозначаем z =(x, y). Множество всех комплексных чисел обозначаем символом С.
Число x называется действительной частью, а y - коэффициентом при мнимой части комплексного числа z. Обозначаем x = Re z, y = Im z.
Комплексно число (x, 0) отождествляется с x, т.е. x = (x, 0). Тогда комплексные числа (1, 0) и (0, 0) отождествляются соответственно с 1 и 0.
Если y ¹ 0, то комплексно число (x, y) называется мнимым, а число (0, y) - чисто мнимым. Число (0, 1) называется мнимой единицей и обозначается символом i.
Определение 1.2. Два комплексных числа z1 =(x1, y1) и z2 =(x2, y2) называются равными, если соответственно равны их действительные части и коэффициенты при мнимых частях, x1 = x2, y1= y2.
Определение 1.3. Суммой комплексных чисел z1 =(x1, y1) и z2 =(x2, y2) называются комплексное число z1 + z2 =(x1 + x2, y1 + y2).
Определение 1.4. Произведением комплексных чисел z1 =(x1, y1) и z2 =(x2, y2) называются комплексное число z1 z2 =( x1x2 - y1y2, x1 y2 + x2y1).
Определение 1.5. Разностью z1 - z2 комплексных чисел z1и z2называются такое комплексное число z, что z2 + z = z1.
Определение 1.6. Частным z1: z2 комплексных чисел z1и z2 называются такое комплексное число z, что z2 z = z1.
Примеры. (2, 1) + (3,-5) = (2+3, 1-5) = (5, -4).
(2, 1)×(3,-5) = (2×3-1×(-5), 2×(-5)+1×3) = (11, -7).
Определение
1.7. Комплексные числа z = (x, y) и 
называются комплексно сопряженными.
Примеры. (2, 1) + (3,-5) = (2+3, 1-5) = (5, -4),
(2, 1)×(3,-5) = (2×3-1×(-5), 2×(-5)+1×3) = (11, -7),
z× 
= (x, y)× (x, -y) = (xx+ y y, x(-y)
+ xy) = (x2 + y2, 0)= x2 + y2,
i×i = (0, 1)×(0, 1) = (-1, 0) = -1.
Теорема 1.1. Множество С всех комплексных чисел является полем относительно операций, определенных выше.
Доказательство. Так как для любых комплексных чисел сумма и произведение определены однозначно, то операции сложения и умножения на множестве С алгебраические. Докажем сначала, что С кольцо (проверим свойства в определениях 3.1).
1. Пусть z1 =(x1, y1), z2 =(x2, y2) , z3 =(x3, y3). Тогда
z1 +( z2 + z3) = (x1, y1) + (x2 + x3, y2 + y3) = (x1 + (x2 + x3), y1 + (y2 + y3)),
(z1 + z2) + z3 = (x1 + x2, y1 + x3) + (x3, y3) = ((x1 + x2) + x3, (y1 + y2) + y3).
По свойствам действительных чисел x1 + (x2 + x3) = (x1 + x2) + x3, y1 + (y2 + y3) = (y1 + y2) + y3. Тогда по определению 1.2 z1 +( z2 + z3) = (z1 + z2) + z3.
2. z1 + 0 =(x1, y1) + (0, 0) = (x1+0, y1+0) = (x1, y1) = z1.
3. Возьмем - z1 =(-x1, -y1). Тогда z1 + (-z1) = (x1, y1) + (-x1, -y1) = (x1+ (-x1), y1+(-y1)) = (0, 0) = 0.
Проверяя свойства 4, 5, 6 по аналогии со свойством 1 получим, что С - кольцо.
Проверим теперь свойства 1-3 в определении 3.4 поля.
1. z1×1 =(x1, y1)×(1, 0) = (x1×1- y1×0, x1×0+ y1×1) = (x1, y1) = z1.
2. z1 z2 =(x1x2 - y1y2, x1 y2 + x2y1) = (x2x1 - y2y1, x2 y1 + x1y2) = z2 z1.
3. Покажем, что для числа z1 =(x1, y1) ¹ (0, 0) существует такое число z =(x, y), что z1 z = 1. В силу определения 1.4 последнее равенство можно переписать в виде ( x1x - y1y, x1 y + xy1) = (1, 0). Тогда по определению 1.2 получим систему
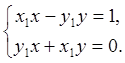
Решая полученную систему
находим 
Тогда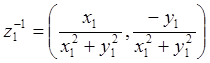 
и z×z-1=1.
Определение 1.7. Любое подполе поля комплексных чисел называется числовым полем.
В силу лекции 1 определения 2.5 для того, чтобы подмножество P Ì С, содержащее число ¹ 0, было числовым полем необходимо и достаточно, чтобы сумма, разность, произведение и частное, если знаменатель не равен нулю, любых чисел из P принадлежали бы P.
Заметим, что наименьшее числовое поле это поле Q рациональных чисел.
Разность комплексных чисел z1 =(x1, y1), z2 =(x2, y2) находится по формуле:
z1 - z2 = z1 +(-z2) = (x1 - x2, y1 - y2). (1.1)
Частное комплексных чисел z1 =(x1, y1), z2 =(x2, y2) ¹ (0, 0) находится
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.