220400 Математический анализ Толстиков А.В.
Курс 1. Семестр 1. Лекция 7. Непрерывность функции в точке
1. Непрерывность функции в точке.
2. Локальные свойства непрерывных функций. Непрерывность сложной функции.
3. Непрерывность обратной функции.
4. Односторонняя непрерывность.
5. Точки разрыва и их классификация.
6. Элементарные функции и их непрерывность.
Литература: Ильин В.А., с.105-127; Письменный Д., с. 130-135. Ермаков В.И., с.197-202. Архипов Г.И., Садовничий В.А., Чубариков В.Н. , с.30-54.
1. Непрерывность функции в точке.
Определение 1. Функция f называется непрерывной в точке a, если она определена в точке a и ее некоторой окрестности и если существует предел этой функции f при x при x ® a, и он равен f(a), т.е.
![]() .
(1)
.
(1)
В силу определений предела это равносильно каждому из следующих утверждений:
1.
![]() ;
;
2. Для любой последовательности {xn}® a при n ® ¥ соответствующая последовательность { f(xn)} ® f(a)
3. f(x) = f(a) + a(x), где - бесконечно малая при x ® a..
4.
![]() (левый и правый переделы функции в точке x =a равны f(a).
(левый и правый переделы функции в точке x =a равны f(a).
Определение 2. Функция f называется непрерывной слева в точке a, если она определена в точке a и в левой половине некоторой окрестности точки a если левый предел этой функции f при x ® a-0 существует и равен f(a), т.е.
![]() .
.
Функция f называется непрерывной справа в точке a, если она определена в точке a и в правой половине некоторой окрестности точки a если правый предел этой функции f при x ® a+0 существует и равен f(a), т.е.
![]() .
.
Теорема 1. Функция f непрерывна в точке a тогда и только тогда, когда функция f непрерывна в точке a слева и справа.
Доказательство. Необходимость. Пусть функция f непрерывна в точке . Тогда по определению 1 для
любой числа e > 0 существует
такое число d > 0, зависящее
от e, d=d(e),
что для любого действительного числа xÎD(f), удовлетворяющего неравенству |x - a| < d, выполняется
неравенство | f(x) - f(a) | < e. Поэтому
для всех xÎD(f), удовлетворяющего
неравенству -d <x
- a £ 0, выполняется неравенство |f(x) - f(a)| < e. Следовательно, ![]() и по определению 2 функция f непрерывна
слева.
и по определению 2 функция f непрерывна
слева.
Далее для всех xÎD(f), удовлетворяющего неравенству 0 £x - a < d, выполняется неравенство |f(x) - f(a)| < e. Следовательно,
![]() и
по определению 2 функция f непрерывна справа.
и
по определению 2 функция f непрерывна справа.
 Достаточность.
Пусть функция f непрерывна слева и справа в
точке а. Возьмем любое число e > 0. Так как
Достаточность.
Пусть функция f непрерывна слева и справа в
точке а. Возьмем любое число e > 0. Так как ![]() , то
существует такое число d1,
что для всех xÎD(f), удовлетворяющего
неравенству -d <x
- a £ 0, выполняется неравенство |f(x) - f(a)|
< e. Так как
, то
существует такое число d1,
что для всех xÎD(f), удовлетворяющего
неравенству -d <x
- a £ 0, выполняется неравенство |f(x) - f(a)|
< e. Так как ![]() , то
существует такое число d2,
что для всех xÎD(f), удовлетворяющего
неравенству 0 £x - a < d, выполняется
неравенство |f(x) - f(a)| < e. Полагаем d = min{d1, d2}. Тогда из указанных свойств следует, что для любого действительного
числа xÎD(f), удовлетворяющего
неравенству |x - a| < d, выполняется неравенство | f(x) - f(a) | < e. По
определению функция f непрерывна в точке a.
, то
существует такое число d2,
что для всех xÎD(f), удовлетворяющего
неравенству 0 £x - a < d, выполняется
неравенство |f(x) - f(a)| < e. Полагаем d = min{d1, d2}. Тогда из указанных свойств следует, что для любого действительного
числа xÎD(f), удовлетворяющего
неравенству |x - a| < d, выполняется неравенство | f(x) - f(a) | < e. По
определению функция f непрерывна в точке a.
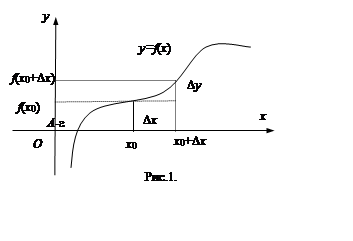
Пусть функция определена в некотором интервале (a, b). Возьмем точки x, x0Î (a, b). Разность x - x0 называется приращением аргумента x в точке x0 и обозначается символом Dx. Отсюда x = x0 +Dx.
Разность f(x) - f(x0)соответствующих значений функции называется приращением функции f(x) в точке x0 и обозначается Dy также или Df или D f(x0): Dy = f(x) - f(x0) = f(x0 +Dx) - f(x0).
Условия
![]() равносильно тому, что приращение Dy
= f(x) - f(x0)
= f(x0 +Dx) - f(x0). бесконечно малая функция при x ® a, т. е.при Dx® 0. Получили утверждение.
равносильно тому, что приращение Dy
= f(x) - f(x0)
= f(x0 +Dx) - f(x0). бесконечно малая функция при x ® a, т. е.при Dx® 0. Получили утверждение.
Теорема 2. Функция f непрерывна в точке x0 тогда и только тогда, когда бесконечно малому приращения аргумента Dx в точке x0 соответствует бесконечно малое приращение функции Dy, т.е.
![]() .
.
Пример 1. Покажем, что функция y = sin x непрерывна в любой точке x Î R.
Рассмотрим произвольную точку и найдем приращение Dy, соответствующее приращению Dx:
![]() .
.
Вычислим предел
![]() , так как произведение
ограниченной функции на бесконечно малую функцию при Dx
®0 есть
бесконечно малая функция при Dx ®0.
, так как произведение
ограниченной функции на бесконечно малую функцию при Dx
®0 есть
бесконечно малая функция при Dx ®0.
2. Локальные свойства непрерывных функций. Непрерывность сложной функции.
Теорема 1. Пусть функции f и g непрерывны в точке x0. Тогда в точке x0 непрерывны функции;
1) f + g;
2) f - g;
3) c1 f + c1g для всех c1 Î R;
4) f g;
5) f /g, если f(x0) ¹0.
Доказательство.
Пусть функции f и g непрерывна точке x0. Тогда они определены в точке x0 и в некоторой окрестности точки x0 ![]() . Тогда
по свойству предела функции в точке получаем
. Тогда
по свойству предела функции в точке получаем
![]() .
.
Следовательно, по определении функция f + g непрерывна точке x0.
Аналогично доказываются остальные утверждения теоремы.
Теорема 2. Пусть функция f(x) непрерывна в точке x0 , функция g(y) непрерывна в точке y0= f(x0). Тогда сложная функция h(x) = g(f(x)) непрерывна в точке x0.
Доказательство.
Пусть функция f(x) непрерывна
в точке x0 , функция g(y) непрерывна
в точке y0=
f(x0).
Тогда функция f(x) определены в точке x0 и в некоторой окрестности точки x0, ![]() , функция g(y) определены в точке y0 и в некоторой окрестности точки y0,
, функция g(y) определены в точке y0 и в некоторой окрестности точки y0, ![]() . По теореме о пределе
сложной функции имеем:
. По теореме о пределе
сложной функции имеем:
![]() .
.
Следовательно, по определении функция h(x) = g(f(x)) непрерывна точке x0.
Теорема 3. Пусть функция f(x) непрерывна в точке x0 , f(x0)¹0. Тогда существует такая d-окрестность точки x0 , в которой функция сохраняет знак, т.е. для любого x Î( x0 -d, x0 +d) имеем f(x0)f(x)> 0.
Доказательство. Пусть функция f(x) непрерывна в точке x0 , f(x0)¹ 0. Полагаем e = |f(x0)|. ¹0. Тогда по определению непрерывности существует такое число d > 0, зависящее от e, d=d(e), что для любого действительного числа xÎD(f), удовлетворяющего неравенству |x - x0| < d, выполняется неравенство | f(x) - f(x0) | < e. Таким образом для любого x Î( x0 -d, x0 +d)имеем -e+ f(x0) < f(x) < e + f(x0) или -|f(x0)|+ f(x0) < f(x) < |f(x0)| + f(x0). Отсюда находим, если f(x0) > 0, то f(x) > -|f(x0)| + f(x0) = -f(x0) + f(x0) = 0, если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.