Производная и дифференциал функции одной переменной

220400                                                  Математический анализ                                        Толстиков А.В.

Курс 1. Семестр 1. Лекция 9. Производная и дифференциал функции одной переменной

1.  Приращение аргумента и приращение функции. Понятие функции, дифференцируемой в точке. Дифференциал функции.

2.  Производная  функции.

3.  Механический и геометрический смысл производной. Геометрический смысл дифференциала.

4.  Правила нахождения производной.

5.  Производная сложной функции.

6.   Производная обратной функции.

7.  Таблица производных.

Литература: Ильин В.А., с.105-127;  Письменный Д., с. 130-135. Ермаков В.И., с.206-217. Архипов Г.И., Садовничий В.А., Чубариков В.Н. , с.98-108. 

1.  Приращение аргумента и приращение функции. Понятие функции, дифференцируемой в точке. Дифференциал функции.

 Пусть функция f определена в некотором интервале (a, b). Возьмем точки x, x₀Î (a, b). Разность x - x₀ называется приращением аргумента x в точке x₀ и обозначается символом Dx. Отсюда x = x₀ +Dx.

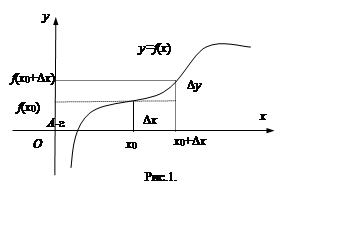
Разность f(x) - f(x₀)соответствующих значений функции называется приращением функции f(x) в точке x₀ , соответствующим приращению аргумента Dx, или просто приращением функции.

Приращение функции зависит от точки x₀ и от приращения аргумента Dx. Обозначается Dy, или Df, или       D f(x₀), или D f(x₀, Dx):

Dy = f(x) - f(x₀) = f(x₀ +Dx) - f(x₀).

Определение 1.  Функция f называется дифференцируемой в точке x₀, если ее приращение в точке можно представить в виде

Dy = A×Dx + a(Dx)×Dx,                                                                 (1)

где A - постоянная, не зависящая от Dx, a(Dx) - бесконечно малая при Dx ®0.

Отметим, что постоянная A и бесконечно малая a(Dx) зависят от x₀. Определение 1 с использованием   символа о-малое может быть записано в виде:

Dy = A×Dx + о(Dx),(1)

при Dx ®0. Последнее равносильно эквивалентности

Dy ~ A×Dx                                                                           (2)

при Dx ®0.

Теорема 1. Если функция f дифференцируемой в точке x₀, то она непрерывна в точке x₀.

Доказательство. Если функция f дифференцируема в точке x₀,  то имеет место равенство (1). Откуда при Dx ®0 получаем, что Dy ®0. Тогда функция f непрерывна в точке x₀.

Замечание. Обратное неверно. Например, функция y =|x|, непрерывна в точке x=0, но не дифференцируема в ней. Действительно, для функции

имеем Dy = |x₀ +Dx| - |x₀|. Отсюда при x= 0 имеем Dy = |Dx| - |0| =|Dx|. Тогда для Dx £ 0 получаем Dy= -Dx+0×Dx и для Dx ³ 0 получаем Dy= Dx+0×Dx. Получили, что коэффициенты у главных частей приращения функции справа и слева от точки Dx =0 различны и функция y = |x|  не дифференцируема в точке 0.

Имеется пример функции, которая непрерывна но дифференцируема в любой точке числовой оси.

Пример 1. Рассмотрим функцию  y = x². Тогда

Dy = f(x) - f(x₀) = (x₀ +Dx)² - x₀ ² = 2x₀ Dx + Dx×Dx  = 2x₀ Dx + о(Dx).

Отсюда следует, что функция дифференцируема на всей числовой оси.

Определение 2.  Пусть функция f дифференцируема в точке x₀,. Дифференциалом приращения D f(x₀), или дифференциалом функции f в точке x₀ называется линейная часть A×Dx приращения функции f в точке x₀.

Дифференциал функции f обозначается символом df, или df(x₀). По определению дифференциала для дифференцируемой функции

df(x₀) = A×Dx.

Дифференциал df(x) можно рассматривать как функцию, зависящую от x и Dx.

Так как приращение функции f(x) = x равно D f = Dx = 1×Dx + 0×Dx, то по определению дифференциала функции Dx = dx .

Пример 2. Дифференциал функции  y = x²  равен df(x) = 2x₀ Dx = 2x₀ dx.  

2.  Производная  функции, ее смысл в различных задачах (механический и геометрический смысл производной). Геометрический смысл дифференциала.

Определение 1.  Пусть функция f определена в некотором окрестности точки x₀.  Производной функции f в точке x₀ называется предел отношения приращения Df(x₀) функции f в точке x₀ к соответствующему приращению аргумента Dx, если приращение аргумента Dx стремится к нулю.

Обозначается производная функции Df(x₀) символами

.

Тогда по определению

.                     (1)

Теорема 1. Если функция f дифференцируемой в точке x₀ тогда и только тогда, когда существует в точке x₀ конечная производная, при этом коэффициент линейной части приращения функции равен f ' (x₀) .

Доказательство. Необходимость. Пусть функция f дифференцируема в точке x₀.  Тогда по определению приращение Df(x₀) функции f в точке x₀ представляется в виде

Df(x₀) = A×Dx + a(Dx)×Dx,

где A - постоянная, не зависящая от Dx, a(Dx) - бесконечно малая при Dx ®0. Отсюда предел

существует, конечен и равен производной функции f  в точке x₀, f ' (x₀) = A.

Достаточность. Пусть функция f  в точке x₀ имеет производную.  Тогда по определению производной существует конечный предел

.

По свойству предела функция бесконечно малая при  Dx ®0. Отсюда

Df(x₀) = A×Dx + a(Dx)×Dx,

где A - постоянная, не зависящая от Dx, a(Dx) - бесконечно малая