Предел функции в точке по Коши и по Гейне. Предел функции на бесконечности. Бесконечно малые и бесконечно большие функции и их свойства

Точка  а называется точкой сгущения области определения функции f, если в любой e-окрестностью  точки а содержится бесконечно много точек области определения функции f.

Определение 3 (Коши). Пусть а - точка сгущения области определения функции f. Точка  A называется пределом функции f(x) при x стремящемся к точке а (обозначаем , если для любой e-окрестностью  точки A найдется такая проколотая d-окрестностью  точки а (зависящая от e) U *(a, e), что образ множестваU *(a, e)ÇD(f) принадлежит  e-окрестности точки A .

O

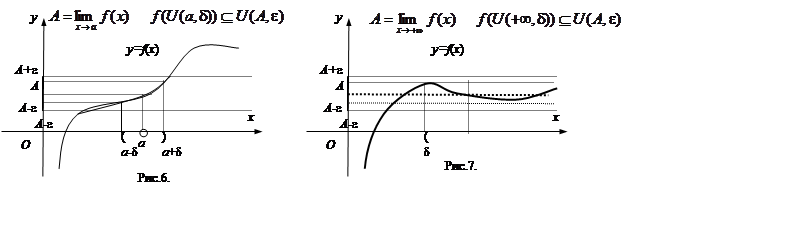На рис. 6 проиллюстрировано определение предела функции при а и А конечных. На рис. 7 проиллюстрировано определение предела функции при А конечном и при а = +¥. Распишем эти определения используя определения окрестностей.

Определение 3.1. Пусть число а - точка сгущения области определения функции f. Число A называется пределом функции f(x) при x стремящемся к числу а (обозначаем ), если для любой числа e > 0 существует такое число d > 0, зависящее от e, d=d(e), что для любого действительного числа xÎD(f), удовлетворяющего неравенству 0 < |x - a| < d, выполняется неравенство | f(x) - A | < e.

Это определение символически можно записать следующим образом:

Пример 1. Доказать, что . Возьмем любое число e > 0 и покажем, что существует такое число d > 0,  что для любого действительного  x, удовлетворяющего неравенству 0 < |x - 2| < d, выполняется неравенство | x² - 4 | < e.  Так как |x² - 4 | =  |x - 2 | | x + 2 | , и при |x - 2| < 1 имеем  -1< x - 2 <1, 3< x+2  <5, | x + 2 | <5. Поэтому возьмем d=min{1, e/5}. Тогда при |x - 2| < d получаем  | x² - 4 | =  | x - 2 | | x + 2 |< 5×e/5 = e. Следовательно, по определению .

Определение 3.2. Число A называется пределом функции f(x) при x ® +¥ (обозначаем ), если для любой числа e > 0 существует такое число d =d=d(e) > 0, что для любого действительного числа xÎD(f), удовлетворяющего неравенству x > d, выполняется неравенство | f(x) - A | < e.

Это определение символически можно записать следующим образом:

Пример 2. Доказать, что . Возьмем любое число e > 0 и покажем, что существует такое число d > 0,  что для любого действительного  x, удовлетворяющего неравенству x > d, выполняется неравенство.  Так как, то доказываемое неравенство равносильно неравенству . При x >0 имеем |x + 1| = x + 1и доказываемое неравенство дает . Поэтому возьмем d=max{0, 1/e - 1}. Тогда получаем  . Следовательно, по определению.

Упражнение.  Для того, чтобы понять и усвоить общее определение предела распишите его во всех остальных случаях (сделайте чертежи). Осталось рассмотреть случаи

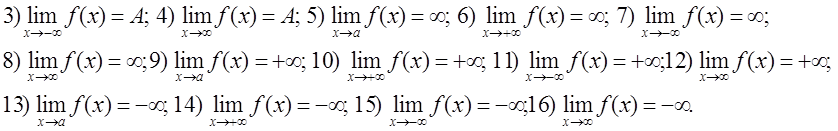
Например, последний предел можно расписать следующим образом.

Определение 3.3. Пусть ¥ - точка сгущения области определения функции f. Точка -¥ называется пределом функции f(x) при x ®¥(обозначаем ), если для любой числа e > 0 существует такое число d=d(e)>0, что для любого действительного числа xÎD(f), удовлетворяющего неравенству |  x |  < -d, выполняется неравенство f(x) < -e.

Это определение символически можно записать следующим образом:

.

Определение предела функции на языке d-e, данное выше, называется определением предела функции по Коши. Часто используется другое определение предела функции, основанное на пределе последовательности.

Определение 4 (Гейне). Пусть а - точка сгущения области определения функции f. Точка  A называется пределом функции f(x) при x стремящемся к точке а, если для любой последовательности {x_n}, сходящейся к a, соответствующая последовательность { f(x_n)} значений функции сходится к  точке A.

Определения предела функции по Коши и по Гейне равносильны.

Теорема  1. Точка  A является пределом функции  f(x) при x ® а по Коши тогда и только тогда, когда Точка  A является пределом функции  f(x) при x ® а по Гейне.

Теорема 2. Если функции  f(x) при x ® а сходится, то она имеет только один предел.

Доказательство.  Допустим, что функция f(x) сходится и имеет два предела A и B при x ® а, A ¹ B. Предположим, что оба предела конечные и точка а  - конечная. Возьмем число e = |A - B|/2. По определению предела существует такое число d₁ >0, что для всех xÎD(f), удовлетворяющих условию 0<|x - a | < d₁ , выполняется неравенство |f(x) - A | < e. Аналогично, По определению предела существует такое число d₂ >0, что для всех xÎD(f), удовлетворяющих условию 0<|x - a | < d₂ , выполняется неравенство |f(x) - B | < e. Полагаем d₂ = min{d₁, d₂}. Тогда при 0<|x - a | < d выполняются оба неравенства и получаем противоречие 2e = |A - B|= |A - f(x)+ f(x) - B |£|f(x) - A |+| f(x) - В |< e+e=2e.

Теорема  3. Предел постоянной функции  f(x) при x ® а по Коши тогда и только тогда, когда Точка  A является пределом функции  f(x) при x ® а по Гейне.

2.  Односторонние пределы.

Определение 1.  Левой половиной e--окрестностью конечной точки а называется интервал