Непрерывные и дифференцируемые отображения. Неявные функции, страница 3

3)  матрица Якоби J_G (X) отображения G находится по формуле J_G (X) = - (J_F (Y))^-1 J_F (X), где J_F (Y), J_F (X) - матрицы Якоби отображения F, отвечающие переменным Y и X соответственно.

Замечание. Теоремы существования и единственности, отмеченные в последнем параграфе предыдущей лекции являются частными случаями этой теоремы.

5.  Теорема об обратном отображении.

Определение 1. Пусть M, K Í Rⁿ, F: М ® K отображение. Отображение G: K ®М называется обратным для отображения , если для любых X Î M, Y Î Kимеем  Y = F(X) Û X = G(Y).

Теорема 1 (теорема о об обратном фуекции) .  Пусть M, K Í R, f: М ® K, функция дифференцируемая на множестве M и ее производная не обращающаяся в ноль на множестве М.  Тогда существует непрерывная обратная функция g: K ®М, т.е. существует такая  функция x = g(y), определенная на множестве K, что g(f(x)) = x для любого xÎK , причем производная обратной функции находится по формуле

.

где y=f(x).

Теорема 2 (теорема о об обратном отображении) .  Пусть M, K Í Rⁿ, F: М ® K, отображение F - гладкое в окрестности точки X = A и невырожденное в точке A.. Тогда существует обратное гладкое отображение G: K ®М,  определенное в некоторой окрестности U(B,d) точки B, т.е. существует такое  отображение G:K ®М, что G(F(X)) = X, причем матрица Якоби J_G (Y) отображения G(Y) находится по формуле J_G  =  (J_F (Y))^-1.

5. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа.

Задача на условный экстремум состоит в следующем: найти экстремум функции

                                                                                            (1)

от n переменных x₁,…, x_n, определенной в области D, если переменные удовлетворяют системе уравнений.

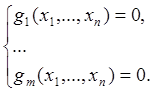                                                                                       (2)

Требуется найти такую точку X₀(x₁⁰,…, x_n⁰)ÎD, которая удовлетворяет системе уравнений (2), и для любой точки X(x₁,…, x_n) ÎD, удовлетворяющей системе уравнений (2) выполняется неравенство f (X) £ f (X₀) для условного максимума (f (X) ³ f (X₀)  для условного минимума).

Определение 1. Пусть в области D определены гладкие функции g_i(X) = g_i(x₁,…, x_n); i = 1,…,m, m < n. Тогда множество D₁Í D всех решений системы уравнений g_i(X) = 0 ; i = 1,…,m , называется многообразием, порожденным функциями g_i(X); i = 1,…,m. Уравнения g_i(X) = 0; i = 1,…,m называются уравнениями связи для многообразия D₁.

Определение 2. Точка А называется точкой условного локального максимума на многообразии D₁, если в некоторой окрестности точки А, для любой точки Х, принадлежащей этой окрестности выполняется неравенство f (X) £ f (X₀) (для условного минимума выполняется неравенство f (X) ³ f (X₀)).

Определение 3. Точка А называется особой точкой функции f (X), если значения всех частных производных в точке А равны нулю и неособой в противном случае ( не все частные производные в точке А равны нулю).

Определение 4. Многообразие D₁, порожденным функциями g_i(X); i = 1,…,m, называется невырожденным, если для любой точки многообразия векторы градиентов , являются линейно независимыми.

Теорема 1(необходимое условие условного экстремума). Если неособая точка А функции f (X) является точкой экстремума для функции f (X) на невырожденном многообразии D₁, порожденным функциями g_i(X); i = 1,…,m, то вектор  

в точке Х = А выражается в виде линейной комбинации градиентов , в этой точке Х = А, т.е. существуют такие действительные числа l₁,…, l_m такие, что

F = G₁l₁ +…+ G_m l_n.

Следствие (метод множителей Лагранжа). Пусть l₁,…, l_m - независимые переменные. Рассмотрим функцию Лагранжа

L(X,L)= f (X) + l₁ g₁(X) +…+ l_m g_m (X).

где L =(l₁,…, l_m). Если неособая точка А функции f (X) является точкой экстремума для функции f (X) на невырожденном многообразии D₁, порожденным функциями g_i(X); i = 1,…,m, то при некотором L = L₀ имеет место равенство

, т.е. все частные производные функции по переменным x₁,…, x_n и l₁,…, l_m обращались в ноль.

Последние условия запишем в виде системы уравнений

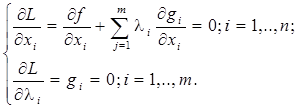                                                               (1)

Решая эту систему находим критические точки с переменными (x₁,…, x_n , l₁,…, l_m). Далее в точке минимума должно выполнятся условие d²F ³ 0 в точке максимума - условие d²F £ 0.