Координатное представление дифференциала dF(X) дифференцируемого отображения F: М ® Rm в силу формулы для дифференциала функции от переменных можно представить в виде (рассматриваем вектор столбцы)
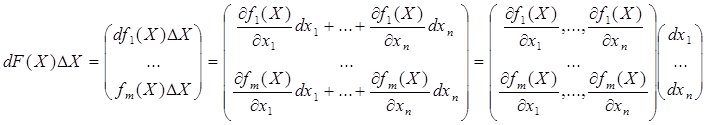. (2)
Определение
2. Матрица 
составленная
из частных производных координатных функций данного отображения F: М ® Rm, определенное
на множестве M Í
Rn , в данной точке
называется матрицей Якоби отображения F в этой
точке X Î M.
Определение 3. Определитель матрицы Якоби отображения F: М ® Rn , M Í Rnв точке X Î M называется якобианом отображения F: М ® Rn , M Í Rnв точке X и обозначается символом
.
Теорема 2. Если отображение F: М ® Rm, определенное на множестве M Í Rn , дифференцируемым во внутренней точке X Î M, то оно то оно имеет в этой точке единственный дифференциал dF(X), который имеет координатное представление (10).
Якобиан отображения линейная функция по каждой координатной функции. Якобиан композиции отображений равен произведению якобианов сомножителей.
3. Условие независимости системы функций.
Определение 1. Система непрерывных функций yi = fi(x1,…, xn); i = 1,…,m, называется функционально независимой в окрестности точки X0 (x10,…, xn0) , если для любой непрерывной функции g(y1,…, ym), определенной в окрестности точки Y0(y10,…, ym0), yi = fi(X0); i = 1,…,m, соотношение
g(f1(x1,…, xn),…, fm(x1,…, xn)) º 0
в окрестности точки X0 возможно только тогда, когда g(y1,…, ym) º 0 в окрестности точки Y0.
Линейная зависимость, рассматриваемая в алгебре. есть независимость по отношению к линейным соотношениям
g(y1,…, ym) = a1y1+…+ am ym.
Если система функций не является функционально независимой, то она называется функционально зависимой.
В случае линейной зависимости условие линейной зависимости векторов равносильно условию, что один из векторов есть линейная комбинация остальных векторов. Аналогичная ситуация имеет место и для функциональной зависимости.
Напомним, что функция от нескольких переменных называется гладкой в области, если она дифференцируема в этой области и все ее частные производные непрерывны в этой области.
Теорема 1. Если
система гладких функций yi = fi(x1,…, xn); i
= 1,…,m, определенных в
окрестности U(X0) точки X0 (x10,…, xn0)
такова, что ранг матрицы Якоби 
в любой точке
один и тот же и равен k, то
1) при k = n система функционально независима в окрестности точки X0;
2) при k < n найдется такая окрестность точки X0 и такие k функций системы, пусть f1,…, fk,что остальные n-k функций системы в этой окрестности представляются в виде
fi(x1,…, xn) = gi (f1(x1,…, xn),…, fk(x1,…, xn) ),
где gi(y1,…, yk); i = 1,…,m - гладкие функции, определенные в окрестности точки Y0(y10,…, ym0), yi = fi(X0); i = 1,…,m, и зависящие только от k координат текущей точки Y = (y1,…, ym).
4. Системы неявных функций. Теорема существования. Дифференцирование неявных функций.
Рассмотрим систему уравнений
.
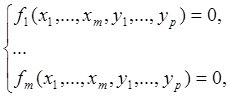(1)
которую будем решать относительно y1,…, ym, т.е. искать локально эквивалентную систему связей вида
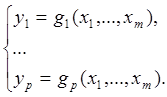(2)
Пусть (X, Y) = (x1,…, xm, y1,…, yp), X(x1,…, xm), Y (y1,…, yp), (A, B) = (a1,…, am, b1,…, bp), A(a1,…, am), B (b1,…, bp), n = m +p. Систему (1) можно записать в виде F(X,Y) = 0, систему (2) в виде Y = G(X), где f1,…, fm координатные функции отображения F, g1,…, gp - координатные функции отображения G.
Определение 1. Пусть m £ n. Дифференцируемое отображение F: М ® Rm, определенное на множестве M Í Rn, называется невырожденным в точке X, если один из миноров порядка m матрицы Якоби отображения F в точке X не равен нулю.
Теорема 1 (теорема о системе неявных функций). Пусть n = m +p и p> 0, и пусть
1) отображение F:М®Rm - невырожденное в точке (A,B), MÍRn, и гладкое в некоторой окрестности U((A,B),e) точки (A, B);
2) F(A, B) = 0;
3)
¹0.
Тогда в некоторой окрестности U(A,d) точки А существует единственное гладкое отображение G(X) = G(g1(X),…, gm(X)), X(x1,…, xm), обладающее следующими свойствами:
1) F(A, G(A)) = 0;
2) для всех X Î U(A,d) имеем F(X, G(X)) = 0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.