







220400 Алгебра и геометрия Толстиков А.В.
Лекции 17. Поверхности и кривые второго порядка
1. Поверхности второго порядка в пространстве R3
2. Поверхности вращения.
3. Цилиндрические поверхности.
4. Конические поверхности.
5. Эллипсоиды.
6. Однополостные гиперболоиды и его прямолинейные образующие.
7. Эллиптические параболоиды.
8. Гиперболические параболоиды и его прямолинейные образующие.
9. Классификация кривых второго порядка.
10. Классификация поверхностей второго порядка.
11. Приведение кривой второго порядка и поверхности второго порядка к каноническому виду по методу собственных значений
Рекомендуемая литература
1. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997.
3. Воеводин В.В. Линейная алгебра.. М.: Наука 1980.
4. Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П.. М.: Наука, 1981.
5. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.
1. Поверхности второго порядка в пространстве R3
Поверхностью второго порядка в пространстве R3 называется поверхность s, определяемая в системе координат Ox1x2x3 уравнением вида:
![]() .
(1)
.
(1)
где aij = aji, Ai ; i, j = 1,2,…,n i, j = 1,2,…,n, B - заданные постоянные числа, коэффициенты при старших членах не все равны нулю. Старшие члены образуют квадратичную форму
f(x1,
x2, x3)
= ![]() , называемую квадратичной формой поверхности.
, называемую квадратичной формой поверхности.
Сначала изучимчастные виды поверхностей второго порядка, а затем рассмотрим преобразование общей поверхности к частным случаям.
2. Поверхности вращения.
Определение 1. Пусть в пространстве дана прямая a и линия l, которая не лежит в плоскости, перпендикулярной прямой a. Поверхность s, которая получается вращением линии l относительно прямой a, называется поверхностью вращения. Линия l называется образующей поверхности вращения, прямые называется осью вращения.
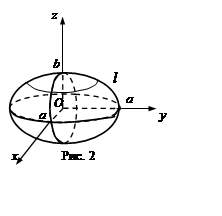 Поверхность
вращения состоит из окружностей, которые получаются вращением точек линии l относительно прямой a, и
которые лежат в плоскостях перпендикулярных прямой a,
с центрами на прямой a.
Поверхность
вращения состоит из окружностей, которые получаются вращением точек линии l относительно прямой a, и
которые лежат в плоскостях перпендикулярных прямой a,
с центрами на прямой a.
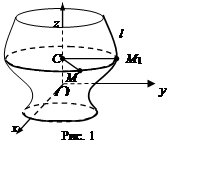 Пусть
образующая l поверхности вращения s лежит координатной плоскости Oyz, и задана уравнением
Пусть
образующая l поверхности вращения s лежит координатной плоскости Oyz, и задана уравнением
f(y,z) = 0, x = 0; (1)
равнение поверхности вращения линии lотносительно оси Oz:
![]() . (3.2)
. (3.2)
Пример 1. Поверхности вращения эллипса относительно оси Oz:
![]() .
(3.3)
.
(3.3)
Полученная поверхность называется эллипсоидом вращения и изображена на рис. 2.
3. Цилиндрические поверхности.
Определение 1. Пусть в пространстве дана линия l и вектор s. Цилиндрической поверхностью s с направляющей l и образующими параллельными s называется множество всех точек прямых параллельных вектору s и пересекающих кривую l. Линия l называется направляющей цилиндрической поверхности s, прямые, из которых состоит цилиндрическая поверхность, называются образующими цилиндрической поверхности s.
 Пусть
направляющая l цилиндрической
поверхности s лежит в
плоскости, параллельной координатной плоскости Oxy, и
задана уравнением
Пусть
направляющая l цилиндрической
поверхности s лежит в
плоскости, параллельной координатной плоскости Oxy, и
задана уравнением
f(x,y) = 0, z = h; (2)
направляющий вектор s = (m,k,n) не параллелен плоскости Oxy, система координат аффинная.. Уравнение цилиндрической поверхности:
![]() . (3)
. (3)
Пример 1. Поверхность, определяемая уравнением
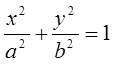 , является цилиндрической и называется эллиптическим цилиндром
(см. рис. 4).
, является цилиндрической и называется эллиптическим цилиндром
(см. рис. 4).
Поверхность, определяемая уравнением
![]() , является цилиндрической и называется гиперболическим цилиндром
(см. рис. 5).
, является цилиндрической и называется гиперболическим цилиндром
(см. рис. 5).
Поверхность, определяемая уравнением
![]() , является цилиндрической и
называется параболическим цилиндром (см. рис. 6).
, является цилиндрической и
называется параболическим цилиндром (см. рис. 6).
4. Конические поверхности.
Определение 1. Пусть в пространстве дана линия l и точка S. Конической поверхностью s с направляющей l и вершиной S называется множество всех точек прямых проходящих через точку S и пересекающих кривую l. Линия l называется направляющей конической поверхностиs, прямые, из которых состоит коническая поверхность, называются образующими конической поверхности s.
Пусть направляющая l конической поверхности s лежит в плоскости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.