Общие вопросы теории оптимизации. Классификация задач математического программирования, страница 8

Вернемся в общей форме записи задачи МП. Общая символическая форма такой записи представлена выражениями (1.3). Очевидно, что такая форма допускает большое разнообразие возможных форм математической постановки задачи. В связи с этим полезно выявить общую структуру постановки задачи математического программирования.

Такая структура в общем случае состоит из трех частей (см. рисунок 1.3).

Первая  часть представляет собой целевую функцию с указанием “направления оптимизации” или  вида экстремума.

Вторая  часть представляет собой ограничения, имеющих форму систем неравенств или уравнений. Поскольку левые части неравенств и (или) равенств могут рассматриваться как некоторые функции, будем в дальнейшем называть такие ограничения функциональными.

Третьячасть представляют собой ограничения, накладываемые непосредственно на значения переменных и (или) требования к множеству (множествам)  таких значений. Они могут быть заданы или в виде указания диапазонов возможных значений, либо в формах, описывающих специфику множеств. Будем называть такие ограничения непосредственными. 

Важной характеристикой задачи МП вида (1.3) является ее размерность, определяемая числом переменных целевой функции n и числом функциональных ограничений m.

Отметим также, что поскольку задача МП имеет ограничения, то она считается задачей условной оптимизации.

 

 

 

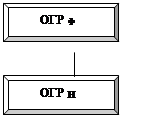Рис. 1.3 -  Общая структура постановки задачи МП

1.5.  Классификация задач математического программирования.

Рассматриваемая классификация позволяет систематизировать многочисленные виды задач МП с целью обоснованного выбора методов их решения.

Классификация задач МП ведется по следующим признакам:

- по виду (характеру) ЦФ ;

- по виду функциональных ограничений (ОГР_ф) (по особенностям функций, задающих ограничения) ;

- по характеру переменных оптимизации и (или) или виду непосредственных ограничений (ОГР_н) ;

- по наличию или отсутствию случайности в исходных данных задачи.

Если целевая функция и функции, входящие в функциональные ограничения, являются линейными, то такая задача МП называется задачей линейного программирования.

З а м е ч а н и е 1.8. Линейными называются такие зависимости, в которые переменные входят в первой  степени и с ними выполняются только действия сложения, вычитания и умножения на число. Линейной называется функция n переменных x₁, x₂ ,…,x_n, определяемая формулой  y = a₁x₁+ a₂x₂ +…+a_nx_n , где a₁, a₂ ,…,a_n  - константы.   

Если в задаче МП нелинейна хотя бы одна функция, то такая задача называется задачей нелинейного программирования.

З а м е ч а н и е 1.9. Нелинейной называется функция, не являющаяся линейной.

В задачах нелинейного программирования выделяется подвид задач выпуклого программирования, в котором, в свою очередь, выделяется подвид задач квадратичного программирования. Одной из разновидностей нелинейного программирования является также геометрическое программирование.

Если в задаче МП переменные оптимизации (все или часть) должны удовлетворять требованию целочисленности, то такая задача называется задачей целочисленного программирования. Существуют целочисленные задачи нелинейного, выпуклого и линейного программирования.

В свою очередь, задачи целочисленного программирования являются подвидом (частным случаем) более широкого класса задач  дискретного программирования.

Целевая функция и левые части ограничений задачи МП могут иметь параметры. Такие параметры, а также правые части ограничений  могут быть случайными величинами. В этом случае рассматриваются задачи стохастического программирования. В свою очередь, в рамках задач стохастического программирования подкласс задач перспективного стохастического программирования, в котором в постановках задач МП случайные величины представляются их математическими ожиданиями  или указываются вероятности выполнения некоторых условий [1,7].

Важно отметить, что задачи МП могут характеризоваться принадлежностью сразу к нескольким введенным выше классам. Так, например, в задаче нелинейного целочисленного программирования  “нелинейность” определяется видом целевой функции, а “целочис-ленность” – характером переменных оптимизации.