Дискретное программирование. Задачи дискретного программирования в САПР. Методы решения задач дискретного программирования

3.   Дискретное программирование

3.1.  Предварительные сведения

Большое количество прикладных задач формально сводится к задачам выбора наилучших значений некоторых параметров из заданного дискретного множества их возможных значений. Такие задачи и методы называются по-разному: целочисленное программирование, дискретное программирование, комбинаторное программирование. Опираясь на мнение авторов монографии [9], будем использовать для обозначения указанного класса задач термин  дискретное программирование (ДП).

Видовой признак «дискретный» отражает  особенности множества, задающего ОДР в задаче МП. Эти особенности состоят в том, что переменные оптимизации x₁,  x₂ , …, x_n  в рассматриваемой задаче являются элементами либо конечных, либо счетныхмножеств [9].

З а м е ч а н и е 3.1.  Множество называется конечным, если оно содержит n элементов, где n - натуральное число. Счетным называется бесконечное множество, для которого существует взаимно однозначное соответствие с множеством натуральных чисел.

З а м е ч а н и е 3.2. Понятию «дискретность» («прерывность») в математике противопоставляется понятие «непрерывность». Задачи ДП выделяются в отдельный класс по признаку «дискретность переменных оптимизации». Тогда остальные противопоставляемые им задачи МП имеющие непрерывные переменные оптимизации, следовало бы  назвать задачами непрерывного программирования. Однако такой термин распространения не получил.

В наиболее общей (теоретико-множественной) форме условие дискретности задается раздельно  по отдельным переменным следующим образом:

x_j Î D _j    ,         j Î J _д                                 (3.1)

где D_j   - конечное или счетное множество,

J_д  - множество индексов переменных оптимизации, для которых задано условие дискретности.

Различают полностью дискретные задачи ДП и частично дискретные задачи ДП. В первом случае  представляет собой множество всех переменных задачи ; во втором случае  является подмножеством множества индексов всех переменных.

Как известно, допустимый план задачи МП может быть представлен в виде n-мерного вектора или точки n-мерного пространства

.

Пусть каждая из переменных x_j  принадлежит конечному множеству: В этом случае  прямое произведение таких множеств

, задающее допустимое множество планов задачи ДП, также будет дискретным множеством.

Важным частным случаем ДП является целочисленное программирование (ЦП).

З а м е ч а н и е 3.3. Целочисленность - частный случай дискретности. (Множество целых чисел включает в себя множество натуральных чисел, число нуль  и множество отрицательных целых чисел).  

В задачах такого типа вводятся (непосредственные) ограничение ОГР_н   вида :

x_j - целые числа  .(3.2)                                                   

Такие ограничения называются  требованиями целочисленности.

По аналогии с (3.1) такие ограничения могут накладываться как на все, так и только на отдельные переменные. Поэтому различают полностью целочисленные и частично целочисленные  задачи ДП.

З а м е ч а н и е 3.4.  Поскольку в состав целых чисел входят также и отрицательные целые числа, то в задачах ДП требование целочисленности, как правило, должно использоваться совместно с требованием  неотрицательности переменной.

Множество целых чисел является бесконечным (счетным). Поэтому выполнение требование целочисленности не обеспечивает конечности множества допустимых решений. Последнее достигается только при совместном использовании этого требования с системой соответствующих функциональных  ограничений ОГР_ф.

Большую роль в ДП играют переменные, которые могут принимать только два возможных значения: 0 или 1. Такие переменные называются  двоичными или  булевыми.

Такие переменные имеют двоякую природу.

С одной стороны, они имеют “арифметическую природу”. Это означает, что их можно рассматривать как целые числа, складывать друг с другом или умножать на действительное число.

С другой стороны, они имеют “логическую природу”. Это означает, что в рамках задач ДП каждому из значений приписывается определенный логический смысл.

Формально двоичные переменные задаются с помощью ограничений одного из следующих видов:

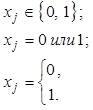                                    (3.3)                                                    

З а м е ч а н и е 3.5. Условия (3.3) можно записать также как сочетание двух условий: 0 £ x _j  £ 1,  x_j – целое.

Для обозначения булевых переменных часто используются специальные символы  b_j .

Использование двоичных переменных позволяет осуществить формальный выбор одного варианта из нескольких возможных. Для этого каждому из возможных вариантов ставится в соответствие некоторая двоичная переменная (варианту j – переменная b_j ) . Далее вводится ограничение вида