8x1+4x2![]() 38;
(3.32)
38;
(3.32)
x1![]() 1, x2
1, x2![]() 8 .
8 .
Для наглядности схему расчета по методу ветвей и границ представляют в виде дерева решений, приведенного на рис. 3.4.
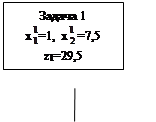 |
х2![]() 7
х2
7
х2![]() 8
8
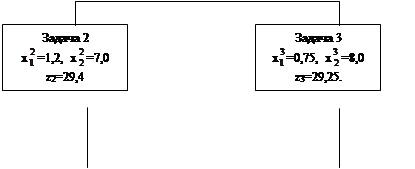 |
![]()
![]()
![]()
![]()
![]() х1
х1![]() х1
х1![]() 2
х1=0 х1
2
х1=0 х1![]() 1
1
![]()
|
|
|
|
||||||||
Рис. 3.4
Корень этого дерева представляет собой исходную задачу (без учета требования целочисленности), а каждая вершина представляет собой подзадачу, полученную при добавлении соответствующего ограничения. В вершинах этого дерева указаны также решения подзадач.
Анализ полученных решений задач ЛП, сформированных при реализации метода ветвей и границ, показывает, что оптимальным решением исходной задачи является решение задачи 5:
x1=2, x2=5, z=29.
Для получения такого решения в рассмотренном примере было осуществлено решение семи вспомогательных задач ЛП, полученных в результате трех ветвлений задач.
З а м е ч а н и е 3.11. Для уяснения технологии рассматриваемого метода рекомендуется выполнить графическое решение задач 1-7.
Приведенный упрощенный пример иллюстрирует процесс ветвления задач. Однако он не отражает другую особенность метода ветвей и границ, состоящую в определения верхних (в случае минимизации – нижних) границ непересекающихся подмножеств, на которые разбивается допустимое множество исходной задачи ЦЛП, а также использование этих значений для организации процесса поиска оптимума. Такие границы оценивают значения ЦФ, которые она принимает на элементах таких множеств.
З а м е ч а н и е 3.12. Верхней границей множества называется любое число s, ограничивающее сверху данное множество действительных чисел М, т.е. обладающее свойством s ³ a, для всех a Î M.
В рассматриваемом методе в качестве верхней границы допустимых множеств принимается значение оптимума ЦФ задачи ЛП zоптЛП , получаемой из задачи (3.12)-(3.15) при отбрасывании условия целочисленности (3.15).
Поскольку введение требование целочисленности, как и любое дополнительное требование, ухудшают значение оптимума ЦФ [1], то значения ЦФ, достигаемые в целочисленных точках, не могут превысить значения zопт ЛП.
Использование верхних границ (оценок) позволяет выделять среди непересекающихся множеств так называемые перспективные множества. В качестве перспективногообычно рассматривается множество, имеющее наибольшую из верхних границ. Именно такие множества в методе ветвей и границ подлежат дальнейшему ветвлению, а неперспективные множества отбрасываются. Это позволяет существенно сократить число решаемых вспомогательных задач и заменить полный перебор всех планов их частичным перебором.
Так, в примере после сравнения оптимумов zопт ЛП задач 2 и 3 (равных соответственно 29,4 и 29,25) в качестве перспективной должна быть выбрана задача 2, а задача 3 должна быть признана неперспективной. При этом дальнейшее ветвление задачи 3 может не производиться.
Рассмотренные приемы ветвления и определения границ не исчерпывают всех особенностей алгоритмов, реализующих метод ветвей и границ. Таким особенностями являются ведение списка задач, выполнение зондирования, определение решения-претендента и др. В связи с этим рекомендуется ознакомиться с полным описанием рассматриваемого алгоритма по [4]. Алгоритм решения задачи ЦЛП методом ветвей и границ более сложен и трудоемок, чем алгоритм метода отсечения. Однако именно он обычно реализуется при построении пакетов прикладных программ для ЭВМ.
Некоторые другие методы решения задач ЦЛП рассмотрены в [9].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.