Дискретное программирование. Задачи дискретного программирования в САПР. Методы решения задач дискретного программирования, страница 6

(Можно сказать, что при выполнении правильных отсечений отсекаются нецелочисленные оптимальные планы, но не отсекается ни один целочисленный план).

После этого решается задача L₁. Затем в случае необходимости добавляется еще одно ограничение и решается задача L₂  и т.д.

Геометрически добавление каждого линейного ограничения отвечает построению гиперплоскости, которая отсекает от многогранника решений предыдущей задачи оптимальную точку с дробными координатами, но не затрагивает ни одной из целочисленных точек этого многогранника.

Таким образом, вместо задачи I решается последовательность задач линейного программирования L₀ = L ,  L₁ ,  L₂ , … , пока решение одной из них не окажется целочисленным. Оно будет одновременно и оптимальным решением задачи  I .

Рассмотрим алгоритм построения отсечения для полностью целочисленных задач (первый алгоритм Гомори). Предположим, что в оптимальном решении задачи L базисными являются первые m переменных. Тогда имеет место базисная система вида

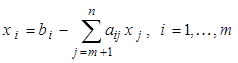.                   (3.16)

Если положить x_j = 0  для  j > m , то получим базисные компоненты оптимального решения .

Рассмотрим некоторую k-ю строку системы уравнений  (3.16) (при этом ее номер совпадает с номером некоторой базисной переменной).

Предположим, что - нецелое и, кроме того, дробным является, по крайней мере, один из элементов  k-ой строки. Представим и все   в виде двух составляющих – целой и дробной части:

;   .          (3.17)

Здесь скобки [ ] означают целую часть числа;  - наибольшее целое, не превышающее . Для любого числа дробная часть f_k по определению удовлетворяет неравенству   .

Так, например, для   имеем   , для  имеем  .

С учетом введенных обозначений k-е уравнение системы (3.16) примет вид

.                        (3.18)

Далее, исходя из требования целочисленности x_k , в [4] выводится соотношение, которому должны удовлетворять дробные компоненты уравнения (3.18). На его основе формируется правильное отсечение, представляющее собой ограничение в форме неравенства, имеющее вид

                                     (3.19)

Такое неравенство для удобства часто записывается  в виде

 ,                                    (3.20)

Пример 3.1.

Построим правильное отсечение для строки базисной системы ограничений, имеющей вид

x₁ = 7/2 - 6/16×x₃  + 2/8×x₄  .

Выделим в коэффициенте ограничений и двух коэффициентах матрицы ограничений целые и дробные части. Получим  

b₁ = 3 + ½ ,  a₁₁ = 6/16 = 0 + 6/16 ,  a₁₂ = - 2/8 = -1 + 6/8.

Построим правильное отсечение по формуле (3.20)

6/16×x₃  + 6/8×x₄  ³ 1/2  

Процесс включения в условия задачи новых ограничений-отсе-чений строится следующим образом. Вычитая из левой части неравенства (3.20) дополнительную неотрицательную переменную x_n+1 и ум-ножая обе его части на -1,  получаем отсечение в виде уравнения

                                 (3.24)        с базисной переменной . Добавляем это уравнение к последней симплекс-таблице предыдущей  задачи.

Решим новую задачу с помощью двойственного симплекс-метода. Если решение окажется нецелочисленным, опять используем последнюю симплекс-таблицу для построения нового ограничения, поступая аналогично до тех пор, пока на очередном шаге не будет получено целочисленное решение.

З а м е ч а н и е 3.10. При реализации метода отсечений с помощью двойственного симплекс-метода необходимо обеспечивать высокую точность вычислений. В связи с этим рекомендуется исходные данные и промежуточные результаты представлять в виде рациональных дробей.  

3.4.4.  Другие методы решения задач ЦЛП

Для решения рассматриваемой задачи применяется также метод ветвей и границ [4,5,9,20]. Он является комбинаторным методом и используется для решения как полностью целочисленных, так и частично целочисленных задач.