Для методов первой группы, называемых методами отсечения, характерно “погружение” их допустимой области в более широкую многогранную область и применении к этой области методов линейного программирования (иными словами, такие методы предполагают временное отбрасывание условий дискретности).
Вторая группа методов, называемых комбинаторными, отличается от первой тем, что в ней, напротив, максимально используется “конечность” задачи, ее комбинаторный характер.
Третья группа методов – это методы случайного поиска и другие приближенные методы.
Аналогичные классификации методов решения задач ДП произведены в работах [4,7,10]. (При этом два первых вида методов выделяются во всех классификациях).
3.4.2. Замечание о решении целочисленных задач
Наиболее изученными задачами дискретного программирования являются целочисленные задачи линейного программирования или задачи целочисленного линейного программирования (ЦЛП).
Постановка задачи ЦЛП отличается от постановки задачи ЛП дополнительным условием целочисленности.
Такие задачи, как и задачи ЛП, допускают геометрическую интерпретацию для ЦФ двух переменных для задачи в стандартной форме. При этом первоначально изображается ОДР задачи ЛП (являющаяся многогранником), а затем в ней выделяются целочисленные точки – узлы целочисленной решетки. Совокупность таких изолированных целочисленных точек и представляет собой ОДР задачи ЦЛП. На основе этой совокупности затем обычно строится целочисленный многогранник, являющийся выпуклой оболочкой конечного множества целочисленных точек. Такой многогранник также имеет крайние точки, являющиеся в данном случае целочисленными.
Так, в двумерном случае планы целочисленной задачи определяются конечным множеством целых точек, лежащих внутри и на границе многоугольника ограничений соответствующей ей обычной задачи ЛП.
Примеры ОДР задачи ЦЛП для случая двух переменных приведены на рис. 3.1
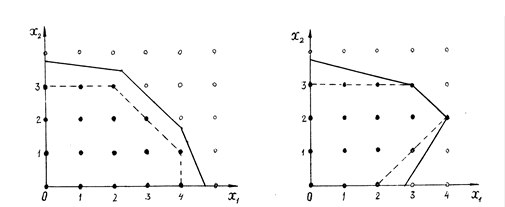
a б
Рис. 3.1
Отметим, что на рис 3.1.а изображен вариант многоугольника ограничений задачи ЛП, граница которого имеет целочисленные точки, принадлежащие только координатным осям, а на рис 3.1.б – вариант, когда граница содержит также и две целочисленные точки, не принадлежащие этим осям.
З а м е ч а н и е 3.9. Целочисленная решетка формируется только для полностью целочисленной задачи. Если не все переменные задачи ЦЛП целочисленные, то ее ОДР будет представлять собой гиперплоскости (для n=2 – линии), ограниченные многогранником задачи ЛП.
Аналогии в изображении ОДР задач ЛП и ЦЛП позволяют перенести на задачи ЦЛП геометрическую интерпретацию и геометрический метод решения на задачи ЛП.
Очевидно, что при движении линии равного уровня z необходимо учитывать только целочисленные точки. Специфической особенностью задач ЦЛП является конечность множества оптимальных точек в случае параллельности линии равного уровня ЦФ и одной из сторон целочисленного многогранника.
Так, например, для задачи ЦЛП, ОДР которой приведена на рис. 3.2а, для трех различных векторов нормали N1, N2 и N3 (сформированных для различных ЦФ) оптимальным планом задачи ЦЛП будут соответственно точка B1 , точка B2 и совокупность точек B1 и B2 .
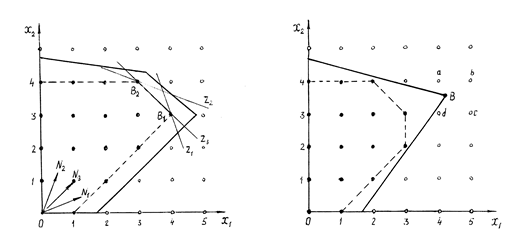
а б
Рис. 3.2
Ограниченность сферы использования геометрического метода решения задачи ЦЛП вызывает необходимость в разработке методов, позволяющих решать задачи ЦЛП для любого n.
В связи с этим возникает естественное предположение о том, что целочисленное решение задачи ЦЛП может быть получено из решения обычной задачи ЛП путем округления нецелых значений компонент вектора Xопт . Однако, в большинстве случаев такое предположение на практике не выполняется.
Такой случай иллюстрируется рисунком 3.2.б. Так, ни одна из целочисленных точек a, b, c и d, находящихся рядом с точкой B (которые могут быть определены в результате округления значений координат точки B), не являются допустимой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.