Пример 7. Исследовать сходимость ряда
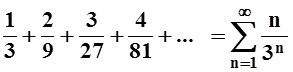 .
.
Решение.
Применим признак Даламбера. Так как 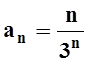 , то
, то 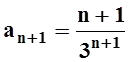 . Вычислим предел:
. Вычислим предел:
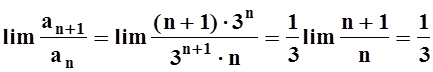 .
.
Так как предел меньше 1, то ряд сходится.
Теорема
8 (признак Коши). Дан ряд ![]() , причём an ³ 0.
Вычислим предел
, причём an ³ 0.
Вычислим предел
![]() .
.
Если p< 1,то ряд сходится, еслиp> 1, то расходится .
Доказательство.
Пусть p<
1. Возьмём число q:
p< q <
1. Из определения предела следует, что ![]() ,
т.е. an < qn. Так как ряд
,
т.е. an < qn. Так как ряд 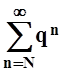 cходится, то, по признаку
сравнения, ряд
cходится, то, по признаку
сравнения, ряд 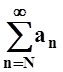 тоже сходится. Но этот
ряд отличается от исходного ряда лишь тем, что отброшены несколько первых
слагаемых. Значит, исходный ряд сходится.
тоже сходится. Но этот
ряд отличается от исходного ряда лишь тем, что отброшены несколько первых
слагаемых. Значит, исходный ряд сходится.
Если ![]() , то
, то ![]() ,
начиная с некоторого номера. Значит, an>1 и lim an ¹ 0. Ряд расходится,
так как нарушено необходимое условие сходимости.
,
начиная с некоторого номера. Значит, an>1 и lim an ¹ 0. Ряд расходится,
так как нарушено необходимое условие сходимости.
Пример 8. Исследовать сходимость ряда
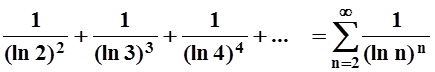 .
.
Решение. Применим признак Коши:
![]() .
.
Так как предел меньше 1, то ряд сходится.
Замечание.
Можно доказать, что признак Коши «сильнее» признака Даламбера. Т.е. если
признак Коши не даёт результата ![]() , то и признак
Даламбера бесполезен
, то и признак
Даламбера бесполезен 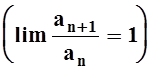 . Но есть примеры, когда
признак Даламбера не даёт ответа, а признак Коши решает задачу. Однако признак
Даламбера применять проще, поэтому он чаще используется.
. Но есть примеры, когда
признак Даламбера не даёт ответа, а признак Коши решает задачу. Однако признак
Даламбера применять проще, поэтому он чаще используется.
Обратим
внимание: имеется очень много общего между сходимостью числовых рядов и
сходимостью несобственных интегралов. Напомним, в 8 модуле для несобственного
интеграла 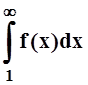 дано определение сходимости,
рассмотрены признаки сравнения –полностью аналогичные признакам сравнения для
числовых рядов. С другой стороны, несобственные интегралы иногда можно
исследовать по определению: вычислить
дано определение сходимости,
рассмотрены признаки сравнения –полностью аналогичные признакам сравнения для
числовых рядов. С другой стороны, несобственные интегралы иногда можно
исследовать по определению: вычислить 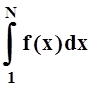 (с
помощью формулы Ньютона – Лейбница), а затем перейти к пределу при N®¥. Поэтому важно научиться исследовать числовые ряды,
опираясь на эту технику.
(с
помощью формулы Ньютона – Лейбница), а затем перейти к пределу при N®¥. Поэтому важно научиться исследовать числовые ряды,
опираясь на эту технику.
Теорема
9 (интегральный признак сходимости). Пусть функция f(x) принимает положительные значения,
монотонно убывает и непрерывна при x ³ 1. Тогда интеграл 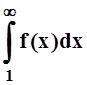 и
ряд
и
ряд 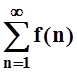 или оба сходятся, или оба
расходятся.
или оба сходятся, или оба
расходятся.
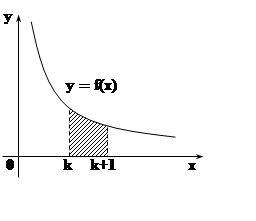 Доказательство.
Пусть k –натуральное число. Так как f(x) убывает, то f(k)
³ f(x) ³ f(k+1) ("xÎ[k, k+1]). Проинтегрируем по отрезку [k, k+1]. Так как
Доказательство.
Пусть k –натуральное число. Так как f(x) убывает, то f(k)
³ f(x) ³ f(k+1) ("xÎ[k, k+1]). Проинтегрируем по отрезку [k, k+1]. Так как 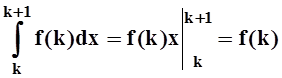 ,
то получим:
,
то получим:
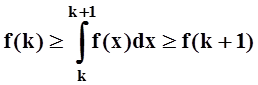 .
.
(Впрочем, эти неравенства легко
следуют из сравнения площадей: 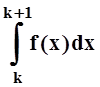 – площадь
криволинейной трапеции, f(k) и f(k+1)
равны площадям соответствующих прямоугольников.)
– площадь
криволинейной трапеции, f(k) и f(k+1)
равны площадям соответствующих прямоугольников.)
Запишем полученные неравенства для k = 1, 2, ..., n и просуммируем их. Сумму интегралов, пользуясь аддитивностью, преобразуем в интеграл по объединению отрезков.
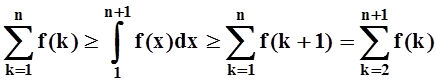 (*)
(*)
Допустим, интеграл 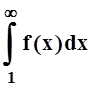 сходится. Это значит, что
существует конечный предел
сходится. Это значит, что
существует конечный предел 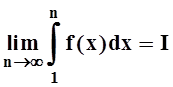 . Так как f(x) ³ 0,
то
. Так как f(x) ³ 0,
то 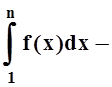 возрастающая последовательность,
т.е.
возрастающая последовательность,
т.е. 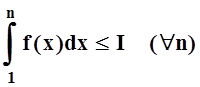 . Используя правую часть неравенства
(*), получим:
. Используя правую часть неравенства
(*), получим: 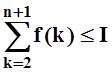 .
Значит, частичные суммы ряда
.
Значит, частичные суммы ряда 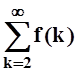 возрастают и
ограничены. Такая последовательность, (см. 1.4.2) всегда имеет предел.
Следовательно, ряд
возрастают и
ограничены. Такая последовательность, (см. 1.4.2) всегда имеет предел.
Следовательно, ряд 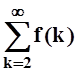 сходится.
сходится.
Обратно,
пусть ряд 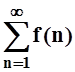 сходится, т.е. существует конечный
предел последовательности частичных сумм:
сходится, т.е. существует конечный
предел последовательности частичных сумм: 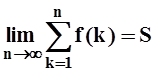 .
Так как эта последовательность, очевидно, возрастающая, то
.
Так как эта последовательность, очевидно, возрастающая, то 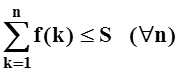 . Отсюда и из левой части (*) следует, что
. Отсюда и из левой части (*) следует, что 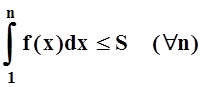 .
Последовательность
.
Последовательность 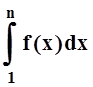 возрастает, ограничена
сверху, а значит имеет конечный предел:
возрастает, ограничена
сверху, а значит имеет конечный предел: 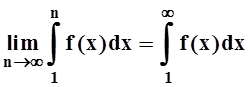 ,
несобственный интеграл сходится.
,
несобственный интеграл сходится.
Пример
9. Исследовать сходимость ряда 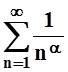 ,
где a–
некоторое постоянное число. Ряд такого вида называется обобщённым
гармоническим.
,
где a–
некоторое постоянное число. Ряд такого вида называется обобщённым
гармоническим.
Решение.
Ясно, что если a£ 0, то 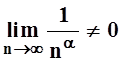 и ряд, конечно, расходится.
Пусть a> 0.
Рассмотрим несобственный интеграл
и ряд, конечно, расходится.
Пусть a> 0.
Рассмотрим несобственный интеграл 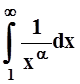 . Все условия
теоремы 9 выполнены, поэтому ряд и интеграл сходятся или расходятся
одновременно (т.е. при одних и тех же a ).
. Все условия
теоремы 9 выполнены, поэтому ряд и интеграл сходятся или расходятся
одновременно (т.е. при одних и тех же a ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.