Здесь мы установим несколько достаточных признаков, позволяющих доказывать сходимость (или расходимость) числовых рядов с положительными членами.
Теорема
5 (признак сравнения). Пусть даны два ряда: ![]() и
и ![]() ,
причём
,
причём
an ³ bn ³ 0 , n = 1, 2, 3, … .
Тогда, если ![]() сходится, то и
сходится, то и ![]() сходится. Если
сходится. Если ![]() расходится, то и
расходится, то и ![]() расходится.
расходится.
Доказательство.
Пусть Sn – частичные
суммы ряда ![]() , S¢n– частичные суммы ряда
, S¢n– частичные суммы ряда ![]() .
Если ряд
.
Если ряд ![]() сходится, то существует конечный
предел S = lim Sn.Так как {Sn}
– возрастающая последовательность, то Sn
£ S ("n).
Из условия следует, что S¢n£ Sn £ S. Поэтому S¢n
– возрастающая ограниченная сверху последовательность. По теореме Вейерштрасса
(см. 1.4.2) она имеет предел. Значит, ряд
сходится, то существует конечный
предел S = lim Sn.Так как {Sn}
– возрастающая последовательность, то Sn
£ S ("n).
Из условия следует, что S¢n£ Sn £ S. Поэтому S¢n
– возрастающая ограниченная сверху последовательность. По теореме Вейерштрасса
(см. 1.4.2) она имеет предел. Значит, ряд ![]() сходится.
сходится.
Если же ![]() расходится, то
расходится, то ![]() не может сходиться (иначе, как мы
доказали,
не может сходиться (иначе, как мы
доказали, ![]() сходился бы), т.е. расходится.
сходился бы), т.е. расходится.
Замечание. Признак сравнения можно применять и в том случае, если неравенство an ³ bn выполняется не для всех n, а лишь начиная с некоторого номера. Действительно, по теореме 1, сходимость ряда не зависит от величины первых нескольких слагаемых.
Пример 5. Исследовать сходимость ряда
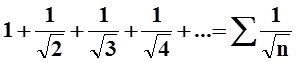 .
.
Решение.
Так как 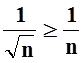 , а ряд
, а ряд ![]() расходится, то, по признаку
сравнения,
расходится, то, по признаку
сравнения, 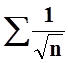 тоже расходится.
тоже расходится.
Теорема
6 (предельный признак сравнения). Даны два ряда: ![]() ,
, ![]() ,
причём an ³ 0, bn > 0. Вычислим предел
,
причём an ³ 0, bn > 0. Вычислим предел 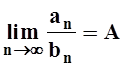 . Если А – конечное ненулевое число, то или оба
ряда сходятся, или оба ряда расходятся.
. Если А – конечное ненулевое число, то или оба
ряда сходятся, или оба ряда расходятся.
Доказательство.
По определению, равенство 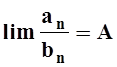 означает, что
означает, что 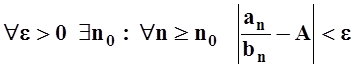 .
.
Последнее неравенство можно записать так:
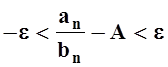 , или
, или 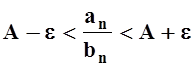 .
.
Учитывая, что bn > 0, получим: начиная с некоторого n0
(A – e) bn < an < (A + e) bn.
Допустим, что ![]() сходится. Тогда, по признаку
сравнения, сходится ряд
сходится. Тогда, по признаку
сравнения, сходится ряд ![]() . (Можно взять e таким, чтобы A – e> 0).
Постоянный множитель A – e, по теореме 2, не влияет на сходимость ряда. Значит,
. (Можно взять e таким, чтобы A – e> 0).
Постоянный множитель A – e, по теореме 2, не влияет на сходимость ряда. Значит, ![]() сходится. Аналогично, если
сходится. Аналогично, если ![]() расходится, то расходится
расходится, то расходится ![]() и, следовательно,
и, следовательно, ![]() . Теорема доказана.
. Теорема доказана.
Пример
6 . Исследовать сходимость ряда 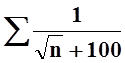 .
.
Решение.
В примере 5 мы установили, что 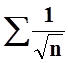 расходится.
Пусть
расходится.
Пусть 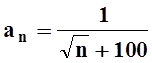 ,
, 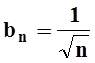 .
Вычислим предел отношения:
.
Вычислим предел отношения:
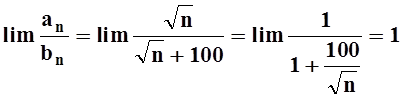 .
.
По теореме 6
«ряды ведут себя одинаково». Значит, 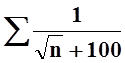 расходится.
расходится.
Замечание.
В теореме 6 ничего не говорится о случаях, когда A = 0 или A = ¥. Однако можно, анализируя
доказательство, сделать полезные выводы и в этих случаях. Пусть, например, A = 0. Используя то,
что, начиная с некоторого номера, an < (A+e)bn,
получаем: если ![]() расходится, то расходится
и
расходится, то расходится
и ![]() . А если
. А если ![]() сходится,
то сходится и
сходится,
то сходится и ![]() . Можно использовать и
такое очевидное соображение: равенство
. Можно использовать и
такое очевидное соображение: равенство 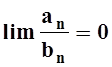 ,
означает, что an = o(bn) , т.е. an стремится к 0 «быстрее», чем bn. Значит, из сходимости
,
означает, что an = o(bn) , т.е. an стремится к 0 «быстрее», чем bn. Значит, из сходимости ![]() вытекает сходимость
вытекает сходимость ![]() .
.
Аналогичные рассуждения можно провести и в случае A = ¥.
Теорема
7 (признак Даламбера). Дан ряд ![]() ,
причём an > 0. Вычислим предел
,
причём an > 0. Вычислим предел
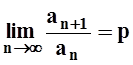 .
.
Если p < 1, то ряд сходится, если p> 1, то ряд расходится.
Доказательство.
Пусть p<
1. Возьмём число q,
лежащее между pи 1: p<
q < 1. Из определения предела следует, что 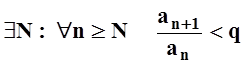 . Это означает, что
. Это означает, что 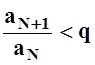 , т.е.
, т.е. ![]() ;
;
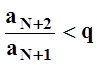 , т.е.
, т.е. ![]() .
Продолжая, получим:
.
Продолжая, получим: ![]() Сравним ряд
Сравним ряд 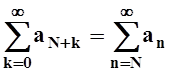 с суммой геометрической прогрессии
с суммой геометрической прогрессии 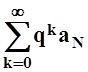 (сходится, так как q<1).
По признаку сравнения,
(сходится, так как q<1).
По признаку сравнения, 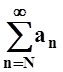 сходится.
Значит, сходится и ряд
сходится.
Значит, сходится и ряд 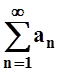 – ведь он
отличается от
– ведь он
отличается от 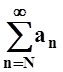 тем, что в
тем, что в 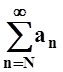 отброшены несколько первых
слагаемых.
отброшены несколько первых
слагаемых.
Если 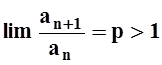 , то
, то 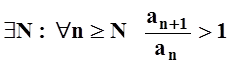 .
То есть начиная с некоторого номера ak+1 >
an. В этом случае, конечно, нарушено необходимое
условие сходимости. Так как
.
То есть начиная с некоторого номера ak+1 >
an. В этом случае, конечно, нарушено необходимое
условие сходимости. Так как ![]() , то ряд
расходится.
, то ряд
расходится.
Замечание.
В признаке Даламбера ничего не говорится о возможности 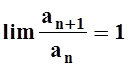 . В этом случае ряд может сходиться,
а может и расходиться, т.е. нужно исследовать его другими методами. Например,
гармонический ряд
. В этом случае ряд может сходиться,
а может и расходиться, т.е. нужно исследовать его другими методами. Например,
гармонический ряд ![]() расходится. Для него
расходится. Для него 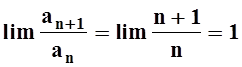 . Мы скоро убедимся, что ряд
. Мы скоро убедимся, что ряд ![]() сходится. А для него
сходится. А для него 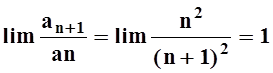 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.