Задачи регрессионного анализа. Многомерная нормальная регрессионная модель. Стратегия регрессионного анализа. Линейная одномерная модель регрессии

Важной является гипотеза H₀ о коэффициенте наклона, H₀ : = 0. В этом случае отклик y изменяется чисто случайно, не завися от значения x. Гипотезу H₀ следует отвергнуть против двусторонних альтернатив 0 на уровне значимости , если число 0 не входит в доверительный интервал для .

Построение доверительных интервалов для параметров b₀ и b₁ основано на том, что отношения и имеют распределение Стьюдента с (n-2) степенями свободы, где b₀ , b₁ - оценки коэффициентов регрессии, полученные при решении нормальных уравнений, S_b0 , S_b1 - оценки стандартных отклонений коэффициентов регрессии.

Тогда доверительные интервалы для параметров и при надежности оценки 1- равны:

и , где - квантиль t- распределения с числом степеней свободы n-2.

Для S_b0 , S_b1 выполняются следующие свойства:

, .

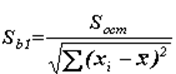Число связей (коэффициентов) для линейной модели равно l=2, поэтому остаточная дисперсия

.

При вычислении S_b1 удобно пользоваться результатом, полученным Бартлетом:

.

Доверительная область линии истинной регрессии. Исключение выбросов

Построим область, ограниченную доверительными границами для средних значений отклика (x). Доверительные пределы отклика для средней точки C( , ) равны границам параметра b₀ , обозначим их через _min и _max . Для коэффициента наклона - через b_1min и b_1max . Через каждую из точек ( , _min ) и ( , _max ) проводятся две прямые с коэффициентами наклона b_1min и b_1max . Искомая область представляет собой максимальную область, охватываемая этими прямыми, она называется также доверительной трубкой. В этой области линия регрессии лежит с вероятностью (1-)². В точке x= границы доверительной области наиболее близки друг другу. Расположение границ показывает, что прогнозы по уравнению регрессии хороши только в случае, если значения x_i не выходят за пределы выборки, по которой вычисляется уравнение регрессии; экстраполяция по уравнению регрессии может привести к значительным погрешностям.

При построении доверительных трубок как для средних значений (x_i ), так и для прогнозов y(x_i ) на графике границы для прогнозов значений новых наблюдений отклика будут более удалены от линии регрессии, чем границы для средних значений. В некоторых случаях выборка, состоящая из точек ( x_i , y_i ) содержит грубые ошибки, "выбросы". Происхождение их может быть самым различным: сбой в работе измерительной аппаратуры, ошибка при переписывании выборочных значений, попадание в данные наблюдений из другого опыта и т.п.

Присутствие ошибочных наблюдений в исходных данных нарушает предпосылки нормальной регрессионной модели и сказывается на результатах расчетов по методу наименьших квадратов. Для исследования влияния выбросов на статистические выводы их надо исключить из обработки, т.е. осуществить "цензурирование" исходных данных. Если при исключении грубого наблюдения возрастает величина коэффициента корреляции и снижается значение остаточной дисперсии, то скорректированная линейная модель более полно представляет исходные данные

Оценка адекватности (значимости) уравнения регрессии позволяет установить, соответствует ли модельное уравнение регрессии Y от экспериментальным данным, и в ряде случаев - существенна ли ошибка от замены истинной регрессии приближенной. После того, как функция приближенной регрессии () найдена, адекватность регрессионной модели проверяется с помощью сравнения критерия, характеризующего разброс эмпирических точек относительно линии или поверхности регрессии, с некоторым пороговым значением.

Глазомерная оценка адекватности

График остатков в случае одномерной линейной регрессии строится для точек (x_i , y_i - b₀ - b₁x_i ) . Глазомерный анализ осуществляется с целью обнаружения в поведении остатков какой-либо зависимости от x. Если остатки разбросаны в горизонтальной полосе, симметричной относительно оси абсцисс, то модель можно рассматривать как адекватную. Если зависимость имеется, то приближенная регрессия (x) не полностью представляет закономерную часть отклика. Видимый линейный тренд означает необходимость введения в модель дополнительного фактора, параболическая зависимость - необходимость добавления квадратичного члена для погашения соответствующей закономерности в поведении остатков.

Для линейной зависимости поверхностной плотности трикотажа y от суммарной длины нитей в петлях x₁ график остатков показывает наличие лишь случайной составляющей.

Разброс наблюдений отклика y_i относительно регрессионной модели можно также наблюдать на графике предсказанных значений. В общем случае, для многофакторных моделей регрессии строится график наблюдаемых значений y_i в зависимости от предсказанных f(x_i1 , x_i2 , x_i3 , ...).

Проверка адекватности линейной однофакторной регрессии при наличии