Определение вероятности ошибки в дискретном канале и пропускной способности дискретного двоичного канала, страница 3

6.  Построить структурную схему кодирующего устройства для выбранного кода.

7.  Определить количество обнаруживаемых и исправляемых ошибок для циклического кода с минимальным кодовым расстоянием d₀ = 3.

Таблица 1

Решение:

Определим длину кодовой комбинации и минимальное число проверочных единичных элементов.

n = 2^m - 1

Число проверочных символов кода (n,k)

r = n - k

Для нахождения минимального числа проверочных символов и соответственно минимальной длины кодового слова, величина m выбирается наименьшей , удовлетворяющей условию   2^m-1 > k

При m=3, условие 2³-1 > 4  выполняется, тогда

n = 2³ - 1 = 7

r = 7 – 4 = 3

Образующий полином должен иметь степень совпадающую с числом проверочных разрядов r. Кроме того, любая разрешенная кодовая комбинация должна делиться на образующий полином без остатка.

Примитивным полиномом называются полиномы для которых характерна зависимость n=2^r-1, это значит что при возникновении ошибки в любом из n разрядов разрешенной кодовой комбинации, число различных остатков будет равно n.

Построим кодовую комбинацию циклического кода.

Отыскание кодовой комбинации F(x) циклического кода (n,k) по заданной последовательности G(x) осуществляется по алгоритму:

-   Находится произведение полинома G(x) на одночлен x^r

-   Полученное произведение делится на образующий полином Р(х).

-   Остаток от деления R(x) записывается после информационных символов.

Для выбора образующего полинома Р(х) воспользуемся таблицей 7.2 (1 стр. 268)

Для r=3 имеем два образующих полинома: (х³+х+1) и (х³+х²+1), соответственно в двоичной записи: 1011 и 1101. Заметим что выбор любого из этих полиномов равноправен, несмотря на то, что в итоге получаются различные кодовые комбинации.

Выберем образующий полином Р(х) = х³+х²+1

Полином описывающий заданную кодовую последовательность:

1010 - G(x) = х³ + 1

G(x) × x^r = ( х³+1 ) × х³ = х⁶ + х³

 

В двоичном коде умножение на х³ соответствует добавлению к исходной комбинации трех нолей.

1010000

Разделим полученное произведение на образующий полином:

Остаток R(x)= х+1

Получаем F(x)= х⁶+х³+х+1

Остаток R(x)= 001

Получаем F(0,1)= 1010001

т.е. сформирована кодовая комбинация F(x) = х⁶+х³+х+1 или F(0,1) = 1010001

Проверим правильность построения кодовой комбинации F(x), путем деления ее на полином Р(х)

Комбинация F(x) найдена верно, т.к. нет остатка.

Построим структурную схему кодирующего устройства для выбранного кода.

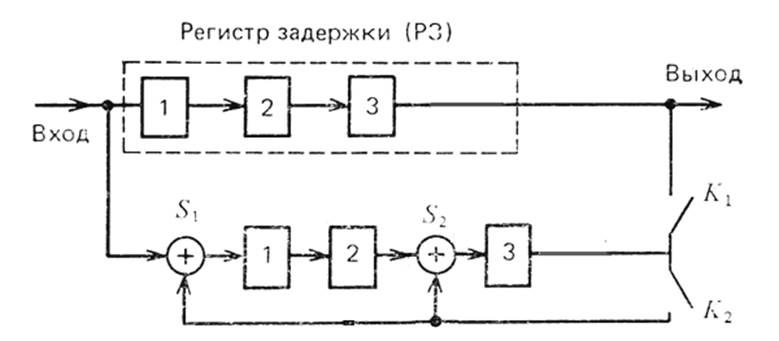
Операция умножения G(x)  на x^rосуществляется сдвигом влево, реализуется регистром задержки с числом ячеек равным r. Операция деления состоит из операции сдвига и сложения по модулю 2 и реализуется регистрами и обратными логическими связями. Число сумматоров по модулю 2 равно r-1.

Определим количество обнаруживаемых и исправляемых ошибок.