Определение вероятности ошибки в дискретном канале и пропускной способности дискретного двоичного канала, страница 2

Задающий генератор (ЗГ) вырабатывает последовательность импульсов высокой частоты fвч. Инвертор и формирователь фронтов (ФФ) импульсов, подключенные к выходу ЗГ, вырабатывают две импульсных последовательности, сдвинутые относительно друг друга на интервал Dt, называемый шагом синхронизации. При отсутствии сигналов с реверсивного счетчика схема добавления закрыта  и не пропускает на выход последовательность fвч. При этом открыта схема исключения и последовательность fвч поступает на один из входов логического элемента "ИЛИ" и далее на делитель частоты, который представляет собой счетное устройство на триггерах. На выходе делителя образуются импульсы тактовой частоты fт. Частота fвч и коэффициент деления выбираются так, чтобы тактовая частота соответствовала частоте следования информационных символов. Информационные символы поступают на вход ФФ, который вырабатывает узкие импульсы на каждый фронт, соответствующие значащим моментам синхронизации (ЗМ). Если частота ЗГ fвч и соответственно тактовая fт уходят в сторону опережения частоты ЗМ на входе второй схемы "И" импульс ЗМ поступит во время положительного полупериода fт и на выходе этой схемы появится сигнал. В это же время первый элемент "И" будет закрыт нулевым уровнем fт. Даже при незначительном опережении тактовой частоты на каждый импульс ЗМ будет срабатывать элемент "И", выход которого подключен к вычитающему входу реверсивного счетчика. Сосчитав несколько импульсов, счетчик выдаст сигнал схеме исключения, та в свою очередь закрывается на время Dt_и, "вырезая" тем самым один импульс из последовательности fвч. Таким образом формирование следующего тактового импульса сдвигается на интервал  Dt (задержка на интервал синхронизации). Если тактовая частота отстает, то срабатывает первый элемент "И" выход которого включен в суммирующий вход реверсивного счетчика. Сосчитав определенное количество импульсов, счетчик вырабатывает сигнал, которым включается схема добавления на период Dt и тем самым добавляется импульс в последовательность fвч на входе схемы "ИЛИ". Делитель частоты выдаст очередной тактовый импульс раньше на время Dt. Таким образом в данном устройстве фазовые сдвиги компенсируются за счет исключений и добавлений импульсов в высокочастотную последовательность fвч. Реверсивный счетчик служит инерционным элементом, то есть исключает нарушение импульсной последовательности fвч при случайных отклонениях ЗМ от своего среднего положения (краевые искажения).

К достинствам данной схемы следует отнести отсутствие обратной связи с генератором, в связи с чем проще обеспечить его высокую стабильность. Это важно прежде всего, когда возникают незначительные перерывы в связи, при этом уход частоты генератора будет минимальным, и время вхождения в синхронизацию незначительным. Второе достоинство - высокая точность синхронизации.

Недостаток данной схемы - трудность реализации при высоких скоростях передачи информации.

Определим частоту задающего генератора.

fвч = m×B = 16×75 =1200 Гц

Определим время синхронизации t_с , при отсутствии краевых искажений

t_с = m × S ×  / 2 × B

Следует отметить, что данная формула учитывает максимальное время синхронизации, т.е. когда расхождение между ЗМ и тактовым импульсом составляет половину периода тактового импульса. Величина  случайная, означает число одинаковых символов идущих подряд, среднее значение  зависит от вероятностей появления символов и длины кодовой комбинации. Примем =2.

t_с = 16 × 2 × 2 / 2 × 75 = 0.427 с

При наличии краевых искажений, время синхронизации возрастает. Определим время вхождения в синхронизм по ф-ле:

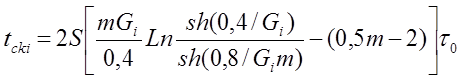
G_i = G₀ +  0,05 i ; при  i = 0, 1, 2.

G₀ = 0,023

G₁ = 0,073

G₂ = 0,123

t₀ - длительность единичного элемента, t₀= 1/В

0,427 c

0,472 c

0,58 c

Задача 3.

Для циклического кода с минимальным кодовым расстоянием d₀ = 3 заданы  число информационных единичных элементов k = 4  и их исходнаяпоследовательность.

Требуется:

1.  Определить минимальное число проверочных единичных элементов r и длину кодовой комбинации n .

2.  Объяснить правило выбора образующего полинома Р(х).

3.  Объяснить, какие полиномы называются примитивными.

4.  Построить кодовую комбинацию циклического кода F(x).

5.  Проверить правильность построения кодовой комбинации циклического кода путем деления F(x) на выбранный образующий полином Р(х).