Исследование методов множественного доступа к каналу связи с прослушиванием несущей и разрешением коллизий, страница 7

Поведение синхронной ALOHA можно теперь описать дискретной цепью Маркова. Пусть n обозначает число узлов с задолженностью в начале заданного окна. Каждый из этих узлов будет передавать пакет в данном окне независимо от других узлов, о вероятностью q_r. Каждый из m-nостальных узлов будет передавать пакет в данном окне, если один (или более) таких, пакетов поступили во время предыдущего окна. Поскольку моменты поступления распределены по пуассоновскому закону со средним l/m,то вероятность непоступления новых пакетов равна е^-l/m; следовательно, вероятность того, что узел, не имеющий задолженности, передаст пакет в данном окне, равна q_a=1-e^-l/m. Пусть Q_a(i,n) обозначает вероятность того, что i, узлов, не имеющих задолженности, передают пакеты в данному окне, и пусть Q_r (i, п)обозначает вероятность того, что i узлов, имеющих задолженность, передают:

                                          (П1.1)

                                          (П1.2)

Заметим, что при переходе от одного окна к другому состояние (т. е. число задолженных пакетов) увеличивается на число новыхпакетов, переданных узлами, не имеющими задолженности, минус один, если пакет передается успешно. Однако пакет передается успешно, если передается только один новый и ни один задолженный пакет или ни один новый и один задолженный пакет. Таким образом, вероятность перехода из состояния пв состояние п + iравна

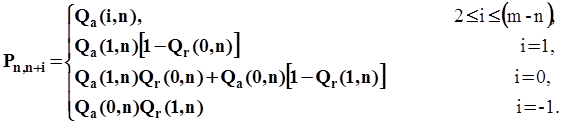               (П1.3)

На рис. П.3 показана эта цепь Маркова. Заметим, что состояние может уменьшиться за один переход не более чем на 1; это позволяет легко вычислить стационарные вероятности с помощью итерации, выразив р_ппри каждом последующем n через р_ои в заключение определив р_о как нормирующий множитель (см. задачу 1). После этого можно найти среднее число узлов с задолженностью и при помощи теоремы Литтла вычислить среднюю задержку.

К сожалению, эта система имеет некоторые очень странные свойства при большом числе узлов и полученные таким образом стационарные распределения и результаты в значительной мере ошибочны. Чтобы это интуитивно понять, заметим, что нам желательно выбрать вероятность повторной передачи q_r достаточно большой, чтобы не допускать больших задержек после конфликтов. Если скорость поступления мала и не очень много пакетов вовлекается в конфликты, то система работает хорошо и повторные передачи, как правило, успешны. Вместе с тем если система попадает в полосу невезения и количество задолженных пакетов n становится настолько большим, что удовлетворяется неравенство q_rn>>1, то конфликты возникают почти во всех последующих окнах и система остается в состоянии большой задолженности долгое время.

Чтобы описать это явление количественно, определим снос в состоянии n (D_n)как среднее изменение задолженности за одно временное окно при старте из состояния n. Таким образом, D_nравно среднему числу новых пакетов, поступивших в систему, минус среднее число успешных передач в окне; среднее число успешных передач равно вероятности успешной передачи, обозначаемой через Р_усп. Таким образом,

                                            (П1.4)

где

                                  (П1.5)

Определим интенсивность попыток G(п) как среднее число попыток передач в окне, когда система находится в состоянии в; имеем

G(п)=(m-n)q_a+nq_r

Если q_aи q_r,. малы. Р_успхорошо аппроксимируется следующей функцией интенсивности попыток:

                                  (П1.6)

Это приближение можно непосредственно получить из (П1.5), используя приближение (1 -х)^y =е^-xy для малых хв выражениях для Q_a, и Q_r,. Аналогично вероятность пустого окна равна приближенно e^-G(т). Таким образом, число пакетов, передаваемых в окне, хорошо аппроксимируется пуассоновской случайной величиной (как и в первоначальном интуитивном анализе), но параметр (n) зависит от состояния. Рис. П1.4 иллюстрирует равенства (П1.4) и (П1.6) в случае q_r>q_a(как выяснится в дальнейшем, только этот случай интересен). Снос равен разности между кривой и прямой линиями. Поскольку снос определяется как среднее изменение состояния при переходе от одного окна к другому, система, хотя и, быть может, флуктуирует, но и среднем движется в направлении сноса и, следовательно, имеет тенденцию к блужданию вокруг двух устойчивых точек с редкими переходами от одной устойчивой точки к другой.