Исследование методов множественного доступа к каналу связи с прослушиванием несущей и разрешением коллизий, страница 10

Псевдобайесовский алгоритм Ривеста представляет особенно простой и эффективный способ адаптации АLOHА. Этот алгоритм, по существу, совпадает с более ранним независимо разработанным алгоритмом Михайлова, но байесовская интерпретация Ривеста проще для понимания. Алгоритм отличается от синхронной ALOHA тем, что новые поступающие пакеты становятся аадолженными сразу в момент поступления. В следующем окне они передаются не с вероятностью 1, а с вероятностью q_r, т. е. так же, как пакеты, уже попавшие в конфликт. Таким образом, если в начале окна число эадолженных пакетов равно п (с учетом только что поступивших), то интенсивность попыток G(n) == nq_r, а вероятность успешной передачи равна nq_r(1-q_r)^n-1. Для нестабилизированной ALOHA эта модификация не имела бы большого смысла, так как qr должна быть относительно малой и новые поступающие пакеты приобрели бы дополнительную ненужную задержку. В случае адаптивной ALOHA, однако, q_rможет повышаться до 1, когда оцениваемая задолженность незначительна, так что новые поступающие пакеты задерживаются только тогда, когда оценка показывает, что система уже перегружена.

Алгоритм работает, производя вычисление оценки и задолженности в начале каждого окна. Каждый задолженный пакет при этом передается независимо с вероятностью . Операция взятия минимума ограничивает q_rсверху единицей и благодаря этому ограничению интенсивность попыток G =nq_rстремится достичь уровня 1. При каждом k оценка задолженности в начале окна k + 1 обновляется исходя из оценки задолженности и сигнала обратной связи в окне k в соответствии с правилом

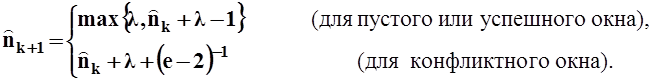   (П1.7)

Добавлением l к предыдущей задолженности учитываются новые поступающие пакеты. Операция взятия максимума обеспечивает, чтобы оценка никогда не была меньше вклада новых пакетов. После успешных передач 1 вычитается из предыдущей задолженности, чтобы учесть успешный уход пакета из системы. Наконец, вычитание 1 из предыдущей задолженности после пустых окон и добавление (е-2)^-1 после конфликтов приводят к тому, что и уменьшается, когда появляется слишком много пустых окон, и и увеличивается, когда возникает слишком много конфликтов. При большой задолженности и  каждый из nзадолжен- ных пакетов независимо передается в окне с вероятностью q_r = l/n. Следовательно, G(n) равна 1 и, согласно пуассоновскому приближению, пустые окна появляются с вероятностью l/e, а конфликты с вероятностью (е - 2)/е, так что уменьшение  

на 1 после пустых окон и увеличение и на (е - 2)^-1 после конфликтов поддерживает в среднем равновесие между п и n^.

Если априорное распределение вероятностей величины n_k является пуассоновским с параметром , то, при условии пустого окна k или успешной передачи в окне k, распределение вероятностей величины n_k+1 является пуассоновским с параметром . При условии конфликта результирующее распределение n_k+1 не совсем пуассоновское, но оно приемлемо аппроксимируется пуассоновским с параметром . По этой причине алгоритм называется псевдобайесовским.

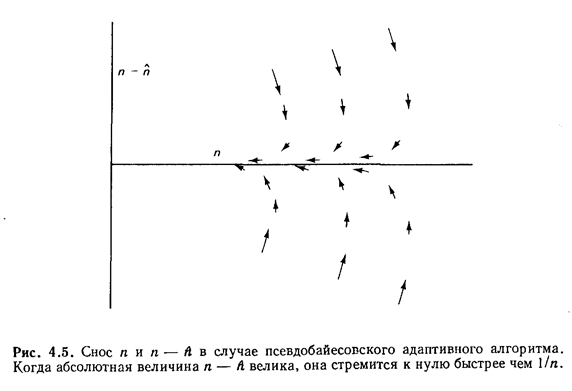
Рис. П1.5 помогает до некоторой степени понять эвристически, почему алгоритм устойчив при l < 1/e. Состояние системы характеризуется величинами п и и и на рисунке показан средний снос этих величин за одно окно. Если nи  велики и равны, то средний снос каждой равен выражению l -1/е, которое отрицательно. Если же абсолютная величина велика, то средний снос п положителен, но среднее уменьшение | значительно больше. Таким образом, если система стартует из некоторой произвольной точки плоскости, в может увеличиваться в среднем в течение некоторого числа окон, но в конце концов сблизятся и тогда nбудет в среднем уменьшаться.

В приложениях скорость поступления l. обычно неизвестна и является медленно меняющейся величиной. Следовательно, алгоритм должен или оценивать l по средней частоте успешных передач или полагать ее равной некоторому фиксированному значению. Михайлов и Цициклис показали, что если в алгоритме скорость поступления пакетов фиксирована и равна 1/е, то система устойчива при всех фактических значениях l, таких, что l< l/e. Никаких строго доказанных результатов не было получено относительно поведения алгоритма в случае, когда используется динамическая оценка l.