Изучите модель сети «синхронная ALOHA», описанной в приложении I и более подробно в книге «Сети передачи данных» Д. Бертсекаса и Р. Галлагера (М.: «Мир», 1989).
ЗАДАНИЕ №1.
Приведите подробный вывод формул для описания переходных вероятностей и стационарного состояния цепи Маркова, описывающей переходы из состояния «k-узлов передает в данном окне» в состояние «l-узлов передает в следующем окне».
Для этого:
(а) Убедитесь в том, что стационарные вероятности рп цепи Маркова, показанной на рис.1, являются решением уравнений
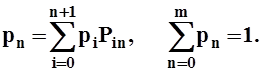
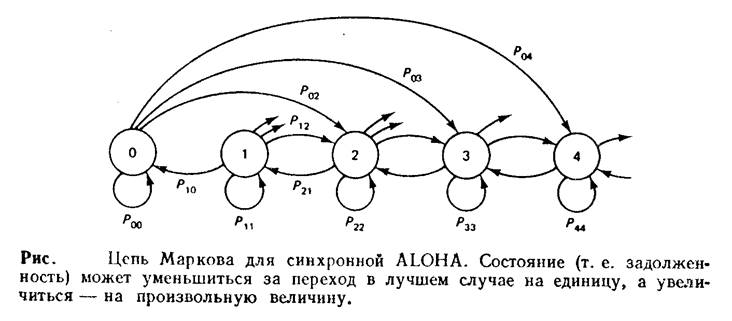 |
(б) Для п<.т используйте а), чтобы выразить pn+1 через р0, p1,...,рп.
(в) Выразите p1 через р0, а затем р2 через p0.
(г) При m = 2найдите выражение для p0, зависящее от переходных вероятностей.
Используя выражения (П1.1-3) для вероятностей передачи i узлами с задолженностями или без задолженностей, и формулы для переходных вероятностей (П1.3) вычислить и отобразить на графиках зависимостей от числа узлов m=2,3,…,7 вероятности что задолженность имеется у двух узлов (вероятность p2).
Пусть n обозначает число узлов с задолженностью в начале заданного окна. Каждый из этих узлов будет передавать пакет в данном окне независимо от других узлов, с вероятностью qr. Каждый из m-nостальных узлов будет передавать пакет в данном окне, если один (или более) таких, пакетов поступили во время предыдущего окна. Поскольку моменты поступления распределены по пуассоновскому закону со средним l/m,то вероятность непоступления новых пакетов равна е-l/m; следовательно, вероятность того, что узел, не имеющий задолженности, передаст пакет в данном окне, равна qa=1-e-l/m. Пусть Qa(i,n) обозначает вероятность того, что i, узлов, не имеющих задолженности, передают пакеты в данном окне, и пусть Qr(i,п)обозначает вероятность того, что iузлов, имеющих задолженность, передают:
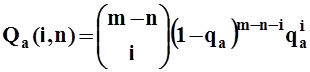 (П1.1)
(П1.1)
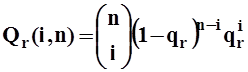 (П1.2)
(П1.2)
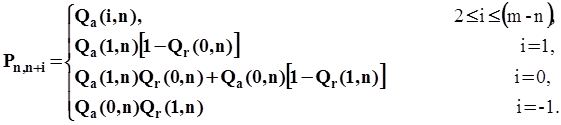 (П1.3)
(П1.3)
Варианты значений параметров для расчета:
(используйте последние две цифры номера зачетки)
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
qa=1-e-l/m. |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,1 |
0,15 |
0,2 |
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
qr |
0,5 |
0,4 |
0,3 |
0,1 |
0,2 |
0,2 |
0,8 |
0, 5 |
0,2 |
2. Определим снос в состоянии n (Dn)как среднее изменение задолженности за одно временное окно при старте из состояния n. Таким образом, Dnравно среднему числу новых пакетов, поступивших в систему, минус среднее число успешных передач в окне; среднее число успешных передач равно вероятности успешной передачи, обозначаемой через Русп. Таким образом,
![]() (П1.4)
(П1.4)
где
![]() (П1.5)
(П1.5)
Определим интенсивность попыток G(п) как среднее число попыток передач в окне, когда система находится в состоянии в; имеем
G(п)=(m-n)qa+nqr
Если qaи qr,. малы. Руспхорошо аппроксимируется следующей функцией интенсивности попыток:
![]() (П1.6)
(П1.6)
Это приближение можно непосредственно получить из (П1.5), используя приближение (1 -х)y =е-xy для малых хв выражениях для Qa, и Qr,. Аналогично вероятность пустого окна равна приближенно e-G(т). Таким образом, число пакетов, передаваемых в окне, хорошо аппроксимируется пуассоновской случайной величиной (как и в первоначальном интуитивном анализе), но параметр (n) зависит от состояния.
(а) Покажите, что Pyспиз (П1.5) можно представить в следующем виде:
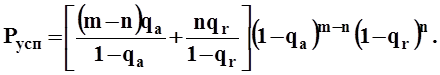
(б) Используя приближение (1 - х)y»е-xyдля малых x, покажите, что при малых qаи qr
![]()
где G(n) = (т - n) qa+nqr.
(в) Заметим, что (1 - х)y = еyln(1-x) . Разложите ln(1 - x)в степенной ряд и покажите, что
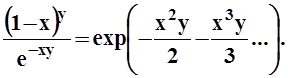
Покажите, что это отношение близко к 1, когда х<<1 и x2y << 1.
ЗАДАНИЕ №3
(а) Изобразите графики зависимостей, показанных на рис. П1.4 Приложения 1, в случае когда qr = l/m, а qa = 1/me.
Варианты значений параметров для построения графика:
(используйте последние две цифры номера зачетки)
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
m |
10 |
15 |
20 |
25 |
20 |
17 |
12 |
8 |
9 |
(б) Найдите скорость ухода (т. е. Русп) в случае всеобщей задолженности n=т.
(в) Обратите внимание на то, что в этом случае не существует неустойчивого равновесия или нежелательной устойчивой точки, и покажите (графически), что это справедливо при любом значении qa.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.