Рассмотрим также
декартову прямоугольную систему координат ![]() , которая
получается из системы координат
, которая
получается из системы координат ![]() поворотом
ее относительно точки
поворотом
ее относительно точки ![]() против
хода часовой стрелки на угол
против
хода часовой стрелки на угол ![]() (Рис. 3.3).
(Рис. 3.3).

Рис. 3.3
Тогда
![]()
![]()
а
осевые моменты инерции сечения ![]() относительно
координатных осей равны
относительно
координатных осей равны
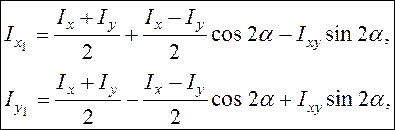
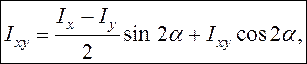
![]()
Действительно,
![]()
![]()
![]()
![]()
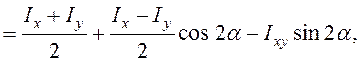
![]()
![]()
![]()
![]()
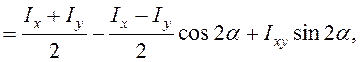
![]()
![]()
![]()
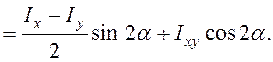
Пусть
![]() главные оси
инерции сечения
главные оси
инерции сечения ![]() . Тогда
. Тогда
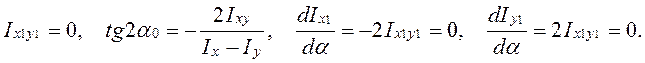
Следовательно,
главные моменты инерции (моменты инерции относительно главных осей) имеют
экстремальные значения по ![]() и
и
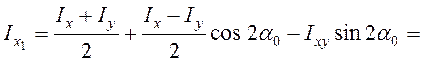
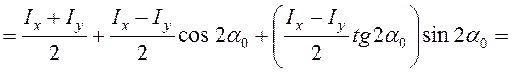
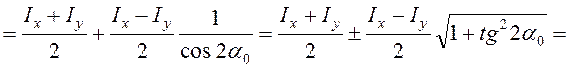
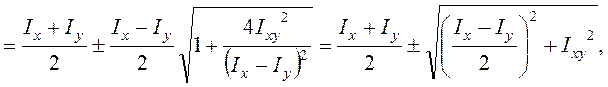
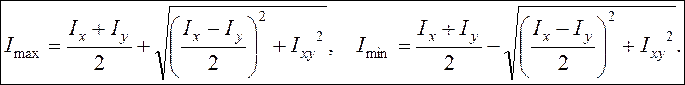
3.4. Моменты инерции простых сечений
Прямоугольник
Рассмотрим прямоугольник высотой ![]() и шириной
и шириной ![]() (Рис. 3.4).
(Рис. 3.4).

Рис. 3.4
Введем декартову прямоугольную систему координат ![]() с началом в
нижнем левом углу прямоугольника, оси которой параллельны сторонам прямоугольника.
Пусть
с началом в
нижнем левом углу прямоугольника, оси которой параллельны сторонам прямоугольника.
Пусть ![]() центр тяжести прямоугольника
(точка пересечения его диагоналей). Координаты центра тяжести равны
центр тяжести прямоугольника
(точка пересечения его диагоналей). Координаты центра тяжести равны ![]() . Введем декартову
прямоугольную систему координат
. Введем декартову
прямоугольную систему координат ![]() ,
оси которой также параллельны сторонам прямоугольника.
,
оси которой также параллельны сторонам прямоугольника.
Тогда осевые моменты инерции сечения ![]() относительно
координатных осей равны
относительно
координатных осей равны
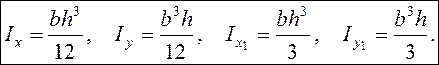
Действительно,
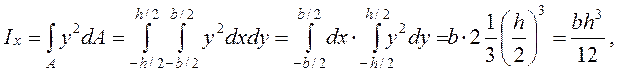
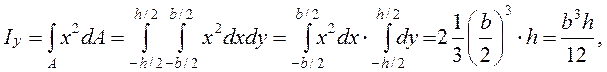
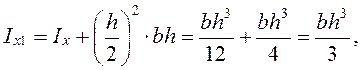
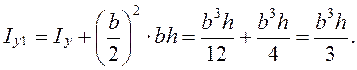
Круг
Рассмотрим круг диаметром ![]() . Введем декартову
прямоугольную систему координат
. Введем декартову
прямоугольную систему координат ![]() ,
начало которой находится в центре круга. Введем также полярную систему
координат
,
начало которой находится в центре круга. Введем также полярную систему
координат ![]() (Рис. 3.5).
(Рис. 3.5).

Рис. 3.5
Тогда осевые моменты и полярный момент инерции круга
относительно осей ![]() и
и ![]() равны
равны
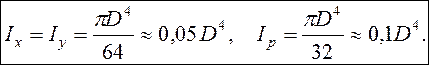
Действительно,
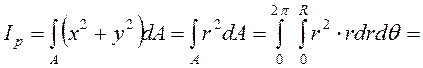
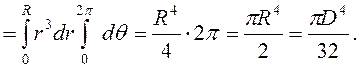
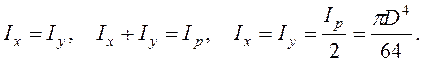
Кольцо
Введем декартову прямоугольную систему координат ![]() , начало которой
находится в центре кольца с внешним диаметром
, начало которой
находится в центре кольца с внешним диаметром ![]() и внутренним
диаметром
и внутренним
диаметром ![]() (Рис. 3.6). Пусть
(Рис. 3.6). Пусть
![]() .
.
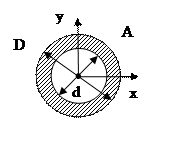
Рис. 3.6
Тогда осевые моменты и полярный момент инерции кольца равны
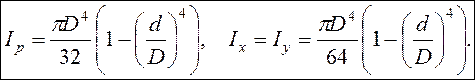
Действительно,
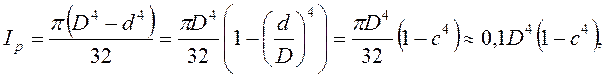
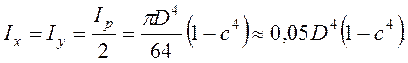
4. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
Центральным растяжением (сжатием) называется вид деформации, при котором в поперечном сечении бруса действует только одна продольная сила, приложенная к центру тяжести сечения. Прямой брус, работающий на растяжение и сжатие, называется стержнем.
Правило знаков. Продольная сила считается положительной, если она вызывает растяжение стержня (Рис. 4.1).
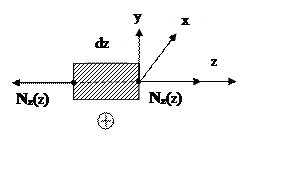
Рис. 4.1
Основные гипотезы: гипотеза о ненадавливании продольных волокон, гипотеза плоских сечений Бернулли, принцип Сен-Венана.
4.1. Закон Гука
Рассмотрим центральное растяжение стержня длины l и квадратного поперечного сечения размером ax b. Приложим к концам стержня растягивающую силу F (Рис. 4.2). Тогда длина стержня увеличиться на Δl. Экспериментально показано, что размеры поперечного сечения уменьшаться - соответственно на (-Δa) и (-Δb).
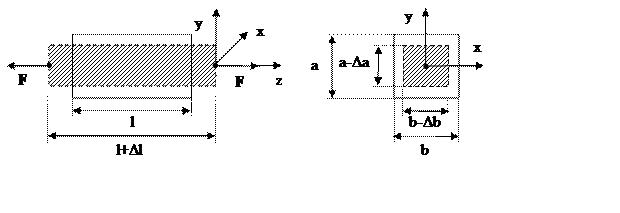
Рис. 4.2
Относительной
продольной деформацией стержня называется безразмерная величина равная ![]() . Обозначим
. Обозначим ![]() . Экспериментально
показано, что
. Экспериментально
показано, что
![]()
где
![]() коэффициент
Пуассона (безразмерная величина),
коэффициент
Пуассона (безразмерная величина), ![]() относительной
поперечной деформация стержня (безразмерная величина).
относительной
поперечной деформация стержня (безразмерная величина).
Пусть ![]() площадь
поперечного сечения,
площадь
поперечного сечения, ![]() нормальное
напряжение.
нормальное
напряжение.
Закон Гука. В пределах упругих деформаций между нормальным напряжением и относительной продольной деформацией существует прямо пропорциональная зависимость
![]()
где
![]() модуль Юнга.
модуль Юнга.
Величина
![]() называется жесткостью
поперечного сечения.
называется жесткостью
поперечного сечения.
Пример
4.1. Пусть стержень длиной ![]() и
постоянного поперечного сечения
и
постоянного поперечного сечения ![]() жестко
закреплен одним концом. Найти абсолютное удлинение стержня при растяжении его
силой
жестко
закреплен одним концом. Найти абсолютное удлинение стержня при растяжении его
силой ![]() (Рис. 4.3).
(Рис. 4.3).
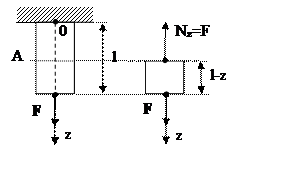
Рис. 4.3
Решение.
Из закона Гука следует, что ![]() .
Откуда получаем формулу Гука
.
Откуда получаем формулу Гука
![]()
Пусть
стержень длины ![]() находится
под действием произвольной системы сил. Мысленно выделим в нем бесконечно малый
участок dz (Рис. 4.4).
находится
под действием произвольной системы сил. Мысленно выделим в нем бесконечно малый
участок dz (Рис. 4.4).
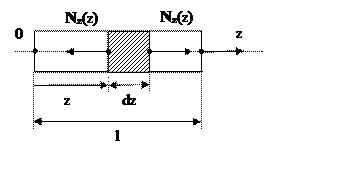
Рис. 4.4
Из формулы Гука следует, что абсолютное удлинение стержня равно
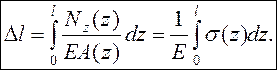
Пример
4.2. Пусть вертикальный однородный стержень длиной ![]() и постоянного
поперечного сечения
и постоянного
поперечного сечения ![]() жестко
закреплен верхним концом и растянут своим весом (Рис. 4.5). Пусть погонный вес
стержня равен
жестко
закреплен верхним концом и растянут своим весом (Рис. 4.5). Пусть погонный вес
стержня равен ![]() . Найти
абсолютное удлинение стержня после деформации.
. Найти
абсолютное удлинение стержня после деформации.
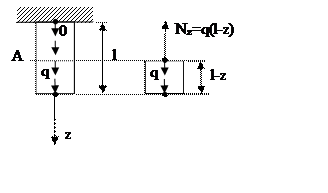
Рис. 4.5
Решение.
Выберем начало координат в точке закрепления стержня. Тогда нормальная сила
равна ![]() . Следовательно,
. Следовательно,
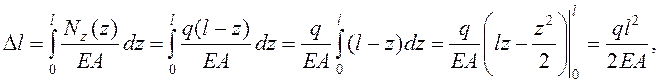
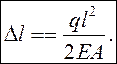
Если
стержень состоит из ![]() различных
участков, то
различных
участков, то
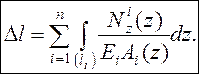
Если
![]() , то
, то
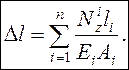
4.2. Статически неопределимые системы
Статически неопределимой системой называется система, в которой внутренние силовые факторы не могут быть определены с помощью только уравнений равновесия статики. Для решения таких задач надо составить уравнения равновесия статики, написать уравнения совместности деформаций и применить закон Гука.
Пример
4.3. Рассмотрим вертикальный стержень, и состоящий из двух участков
длиной ![]() . Пусть жесткости
участков соответственно равны
. Пусть жесткости
участков соответственно равны ![]() и
и
![]() (Рис. 4.6).
Приложим в середине стержня силу
(Рис. 4.6).
Приложим в середине стержня силу ![]() .
Найти реакции опор стержня.
.
Найти реакции опор стержня.
Решение.
Обозначим верхнюю и нижнюю реакции опор стержня соответственно через ![]() и
и ![]() . Мысленно
отбросим верхнюю опору. Тогда уравнение равновесия стержня имеет вид
. Мысленно
отбросим верхнюю опору. Тогда уравнение равновесия стержня имеет вид
![]()
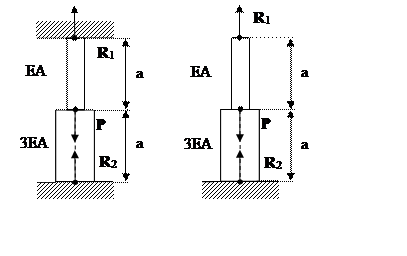
Рис. 4.6
Удлинения стержня от силы ![]() и реакции опоры
и реакции опоры ![]() (формулы Гука для
участков
(формулы Гука для
участков
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.