График зависимости состава пара от состава жидкой фазы при постоянном давлении. Вариантность системы в азеотропной точке

Домашняя работа №1. Вариант 13

Дана зависимость составов жидкой фазы и находящейся с ней в равновесии пара от температуры для двухкомпонентной жидкой системы А – В при постоянном давлении. Молярный состав жидкой фазы x и насыщенного пара y выражен в процентах вещества А. По приведенным данным :

1.  постройте график зависимости состава пара от состава жидкой фазы при постоянном давлении.

2.  постройте диаграмму кипения системы А – В.

3.  определить температуру кипения системы с молярной долей a % вещества А. Каков состав первого пузырька пара над этой системой; при какой температуре закончиться кипение системы; каков состав последней капли жидкой фазы?

4.  определите состав пара, находящегося в равновесии с жидкой фазой, кипящей при температуре Т₁ .

5.  при помощи какого эксперимента можно установить состав жидкой бинарной системы, если она начнет кипеть при температуре Т₁ при наличии диаграммы кипения системы.

6.  какой компонент и в каком количестве может быть выделен из системы, состоящей из b кг вещества А и с кг вещества В.

7.  какого компонента и какое количество необходимо добавить к указанной в п. 6 смеси, чтобы получилась азеотропная система.

8.  какое количество вещества А будет в парах и в жидкой фазе, если 2 кг смеси с молярным содержанием a % вещества А нагреть до температуры Т₁.

9.  Определить вариантность системы в азеотропной точке.

№ варианта	Система	Р*10-4, Па	Молярная доля А,%		Т, К
			x - жидкая фаза	у - пар
13	A - С3Н6О    B - СН3ОН	10,133	0,00	0,0	337,7
			4,8	14,0	335,9
			17,6	31,7	333,1
			28,0	42,0	331,3
			40,0	51,6	330,2
			60,0	65,6	329,1
			80,0	80,0	328,6
			95,0	94,0	328,6
			98,2	97,6	329,1
			100,0	100,0	329,5

[1], стр. 302

№ варианта	T1	a	b	c
13	329,25	60	73	27

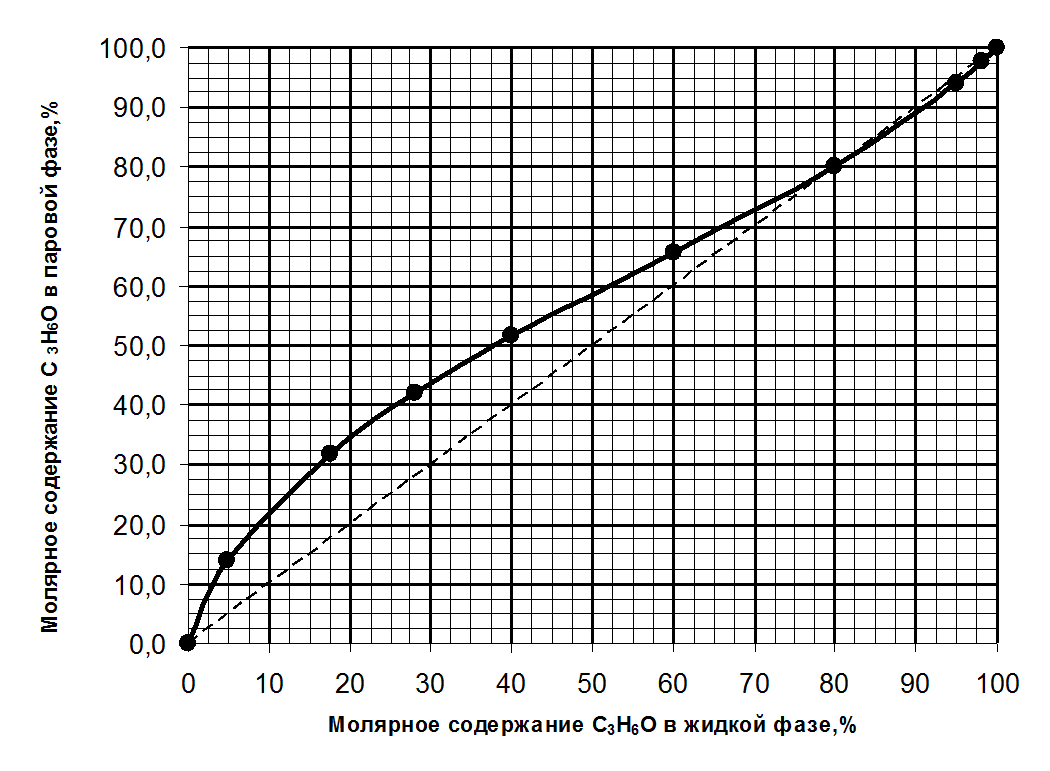
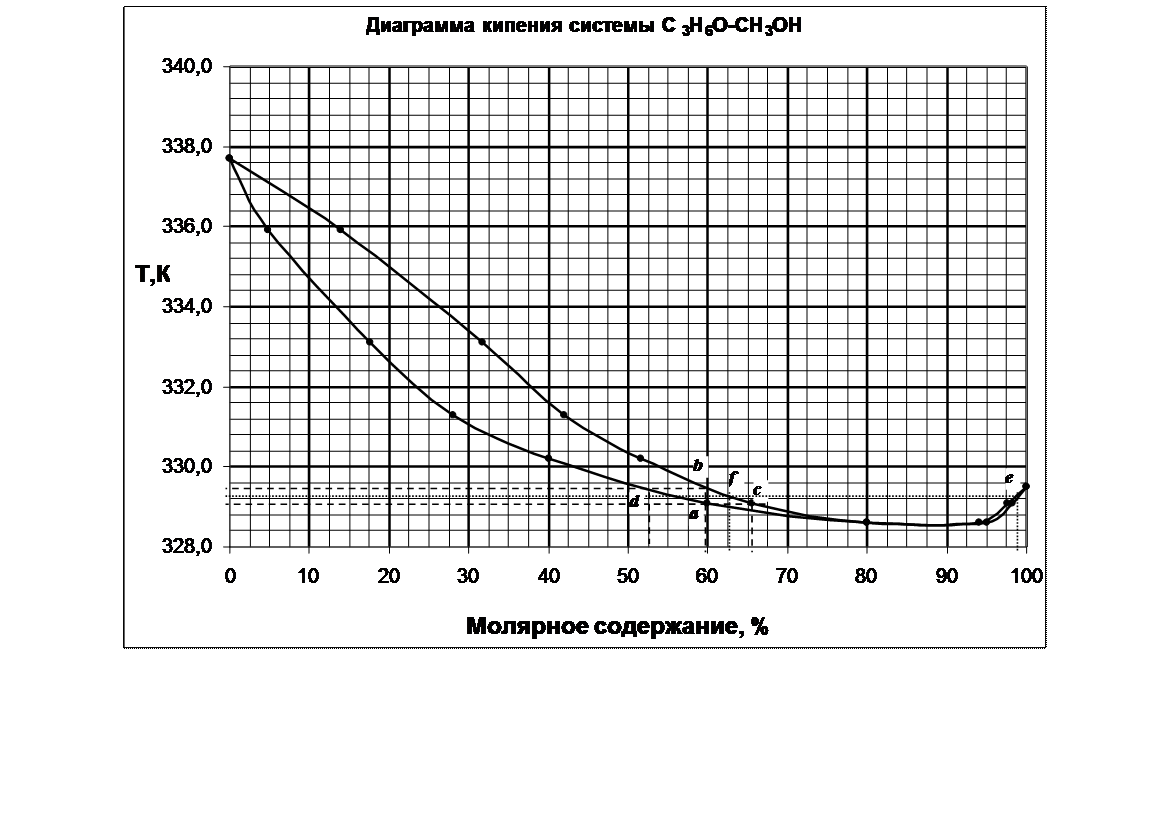
3.  Определение температуры кипения системы с молярной долей 60 % С₃Н₆О.

Для определения температуры кипения системы необходимо провести перпендикуляр от оси Х, соответствующий содержанию в системе 60% С₃Н₆О. Пересечение перпендикуляра с кривой состава кипящей жидкости (нижней кривой диаграммы) показывает точку начала кипения системы – a, соответствующей температуре 329,1 К. Вплоть до 329,1 К система жидкая, гомогенная. При 329,1 К начинается кипение системы, состоящей из 60% С₃Н₆О и 40% СН₃ОН. Для определения состава паровой фазы необходимо провести изотерму через точку а. Пересечение изотермы с кривой насыщенного пара показывает состав пара (точка с) – 66% С₂Н₆О и 34% СН₃ОН. (Это будет состав первого пузырька пара над системой). Состав пара богаче С₂Н₆О, чем жидкость. Следовательно, жидкая фаза обедняется С₃Н₆О и ее состав меняется по линии ad. Состав пара меняется по линии cb. В точке b (при Т≈329,5)вся жидкая фаза превратиться в пар (отсюда, 329,5 – температура конца кипения). Состав пара сравняется с исходной жидкостью (60% С₃Н₆О). Состав последней капли жидкой фазы определяется по точке d – примерно 53 % С₃Н₆О и 47% СН₃ОН.

4. Определение состава пара, находящегося в равновесии с жидкой фазой, кипящей при температуре 329,25 К.

Проводим изотерму Т=345 К, ее пересечение с кривой состава паровой фазы дает 2 точки –  fиe. По ним определяем состав парообразной фазы. Соответственно 63% С₃Н₆О и  37% СН₃ОН (слева от азеотропной точки) и 98% С₃Н₆О и 2% СН₃ОН (справа от азеотропной точки).

5. При помощи какого эксперимента можно установить состав жидкой бинарной системы, если она начнет кипеть при температуре Т₁ при наличии диаграммы кипения системы.

К исходной смеси необходимо добавить какой-нибудь из компонентов, например компонент А и снова измерить температуру кипения. Если Т_кип уменьшиться по сравнению с Т₁, значит система содержала недостаток А по сравнению с азеотропной смесью и ее состав определяем по левой части диаграммы (ок. 63% С₃Н₆О), в противном случае – содержала недостаток В и состав определяется по правой части диаграммы (98% С₃Н₆О).

6. Какой компонент и в каком количестве может быть выделен из системы, состоящей из 73 кг С₃Н₆О и 27 кг СН₃ОН.

∑n =  1,09 + 0,84 = 1,93 кмоль

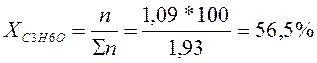
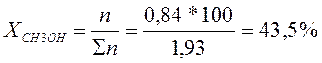
Так как заданный состав находиться слева от азеотропной точки, то выделить ректификацией в чистом виде можно только СН₃ОН. Весь С₃Н₆О (1,09 кмоль) перейдет в азеотропную смесь с молярным содержанием 80%. (Азеотропная точка определяется по графику на пересечении линий жидкого и твердого состояния). Остальные 20% в азеотропном растворе составит СН₃ОН.

Определим количество СН₃ОН, перешедшего в азеотроп:

1,09 кмоль   -  80%

x                  -  20%

 

Тогда в чистом виде можно выделить 0,84 – 0,27 = 0,57 кмоль или 0,57*32 = 18,2 кг СН₃ОН.

7. Какого компонента и какое количество необходимо добавить к указанной в п. 6 смеси, чтобы получилась азеотропная система.

В п.6 система состоит из 56,5% С₃Н₆О и 43,5% СН₃ОН. Азеотроп состоит из 80% С₃Н₆О и 20% СН₃ОН. Метанол в системе находится в недостатке, относительно азеотропа, следовательно, к системе необходимо добавлять С₃Н₆О, чтобы получить из исходной системы азеотропную.

Число моль СН₃ОН в азеотропе – 0,84 кмоль, что составляет 20%. Тогда пропорцией найдем количество С₃Н₆О в азеотропе.

 

Тогда количество бензола, которое необходимо добавить к исходной системе 3,36 – 1,09 = 2,27 кмоль или 2,27*58 = 131,6 кг

8. Какое количество вещества С₃Н₆О будет в парах и в жидкой фазе, если 2 кг смеси с молярным содержанием 60% С₃Н₆О нагреть до температуры 329,25 К.

Сначала определим количество молей вещества, которое содержится в системе массой 2 кг. Для этого вычислим среднюю молекулярную массу: М_ср = 58*0,6 + 32*0,4 = 47,6.

В 2 кг содержится 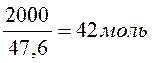 С₃Н₆О и метанола.

По диаграмме определяем молярный состав жидкой и парообразной фаз системы при Т=329,25 К  при содержании в исходной жидкости 60% С₃Н₆О – 56% С₃Н₆О в жидкой и 63% С₃Н₆О - в парообразной.

По правилу рычага определяем количество С₂Н₆О:

                              

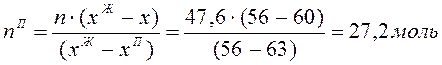
Тогда

9. Определить вариантность системы в азеотропной точке.

С = 2 – 2  + 1 – 1 = 0

Вариантность в азеотропной точки равна 0, т.е. инвариантна.

Литература:

[1] «Сборник примеров и задач по физической химии», Киселева Е.В., Каретников Г.С., изд. 4, 1976 г., 381 стр.