Метод сечений для приближенного вычисления. Задача Гриффитса. Коэффициент интенсивности напряжений

Метод сечений для приближенного вычисления К_I

Широко известный в строительной механике метод сечений может быть с успехом использован в механике разрушения для вычисления коэффициента интенсивности напряжений. При этом в плоской задаче о трещине выделяют часть тела воображаемым сечением (которое может быть ломаным) таким образом, чтобы это сечение проходило через конец трещины.

Далее записывают условия равновесия внешних и внутренних сил, действующих на оставшуюся часть тела. Дополнительное усилие, возникающее у конца трещины в результате повышения напряжений, равно  , где размер α можно определить из условия, что σ_Θ при r=α равно номинальному напряжению. Итак, условие равновесия сводится к тому, что усилие, не передающееся через линию трещины, компенсируется дополнительным усилием от концентрации напряжений у вершины трещины. Рассмотрим вычисление коэффициента интенсивности с помощью метода сечений на конкретных примерах.

  Пример 3.1. Дано: задача Гриффитса. Бесконечная пластина с одиночной трещиной длины 2L растягивается равномерно распределенным напряжением σ перпендикулярно линии трещины. Требуется определить коэффициент интенсивности напряжений.

Решение. Усилие, не передающееся через трещину, равно 2L, а возросшее напряжение у концов трещины создает дополнительное усилие, равное . Размер α можно найти из условия

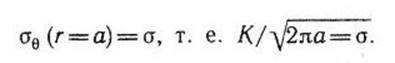
Отсюда

и условие равновесия имеет вид.

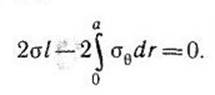
Подставляя сюда напряжения σ_Θ=, находим значение коэффициента интенсивности напряжений К=, которое в данном случае совпадает с точным его значением.

Пример 3.2. Дано: растянутая пластинка конечной ширины с центральной трещиной.

Требуется определить коэффициент интенсивности напряжений и сравнить с задачей Гриффитса.

Решение. Оценим величину поля напряжений, возмущенного наличием трещины. Для бесконечной пластины размер возмущенной зоны перед концом трещины равен α=L/2. При ширине пластины Ь≥2L+2 α =3L конечность ее ширины не влияет на коэффициент интенсивности К=σ. Если же пластина имеет меньшую ширину, т. е. Ь<3L, то из условия равновесия имеем

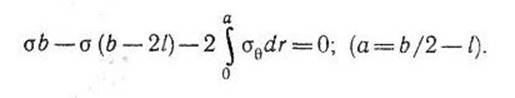
Откуда коэффицинент  интенсивности

Известная формула Ирвина, учитывающая конечность ширины, имеет вид

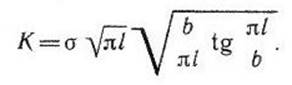
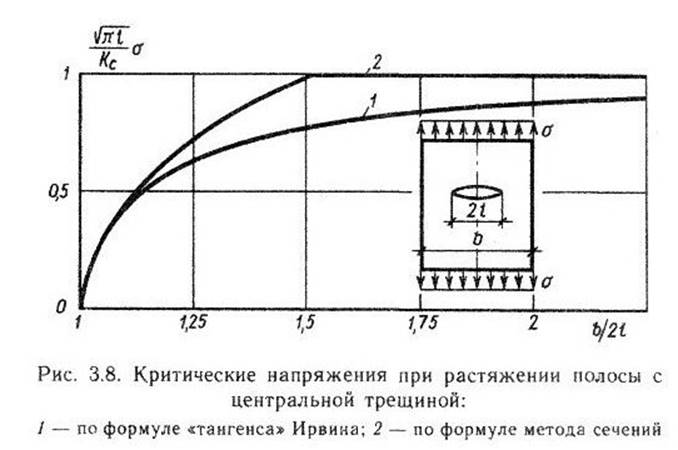
Эти две зависимости приведены на рис. 3.8, где по оси ординат отложено относительное критическое напряжение σ_с К т.е.по сути дела, предельные напряжения в рассматриваемой задаче в долях от предельных напряжений в задаче Гриффитса. Из графиков видно, что по сравнению с формулой Ирвина приближенный метод дает несколько повышенный результат.

Пример 3.3. Дано: бесконечная пластина с трещиной, нагруженная двумя равными и противоположно направленными силами Р, расстояние между точками положения сил равно 2L. Прямолинейная трещина расположена вдоль линии симметрии. Требуется определить коэффициент интенсивности напряжений в зависимости от относительного расстояния между точками приложения сил.

Решение. Искомое сечение проводим по прямой, совпадающей с линией трещины. Уравнение равновесия:

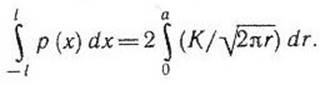
Здесь

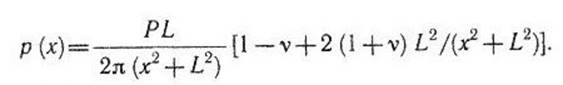
Величина р(х) - напряжение на месте трещины в сплошном теле. Верхний предел интегрирования находим из равенства К/ =p(l). После интегрирования получаем (с = l/L) следующий результат:

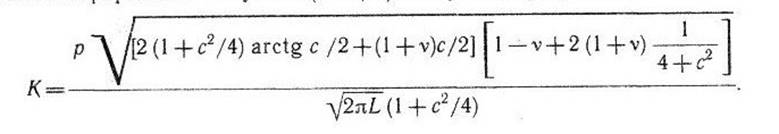
Точное решение, согласно Г.И. Биренблатту, имеет вид

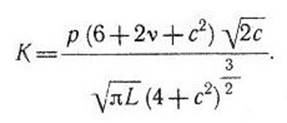
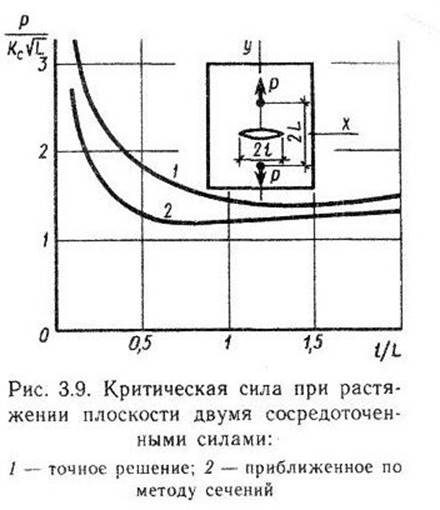
На рис. 3.9 силы для предельного состояния равновесия получены из обычного условия К=К_с, и по оси ординат отложена относительно критическая сила Р/К_с. Сопоставление приближенного и точного решений показывает, что приближенное решение дает для усилий (при данном с) результат, заниженный примерно на 20 %, в то время как качественная картина одинакова - до некоторого значения длины (определяемого минимум кривой) состояние равновесия тела с трещиной неустойчивое (падающая ветвь кривой) , а с увеличением с тело с трещиной переходит в устойчивое состояние (восходящая ветвь).

Пример 3.4. Дано: бесконечная плоскость, ослабленная двумя трещина ми, расположенными вдоль действительной оси. Длина трещин равна 2L₁ и 2L₂. Равномерное растягивающее напряжение направлено перпендикулярно линии трещин. Требуется определить коэффициент интенсивности напряжений