Основная система метода перемещений. Минимальная частота свободных колебаний системы при загружении рамы точечными массами

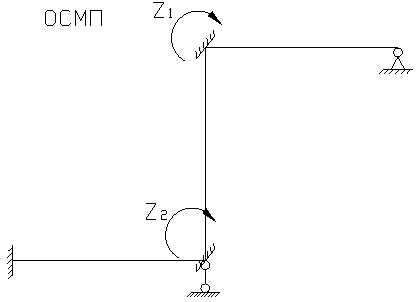
1.

Принимаем основную систему метода перемещений.

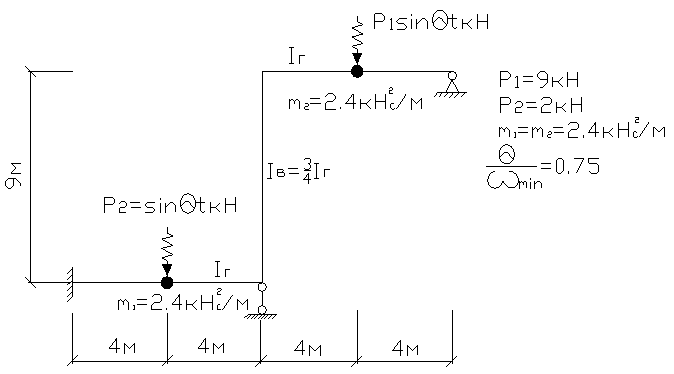
2. Определяем минимальную частоту свободных колебаний системы при загружении рамы точечными массами m₁ и m_2.

Составим частотное ( вековое) уравнение.

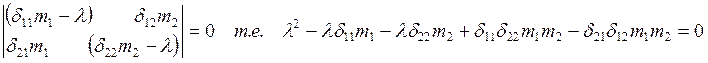
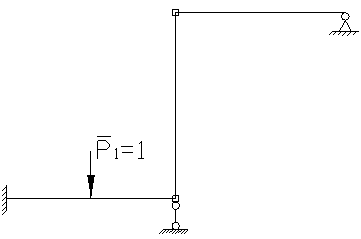
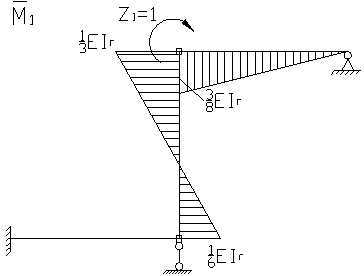
2.1 Для определения коэффициентов векового уравнения построим эпюру моментов в заданной системе от силы  приложенной в направлении возможных колебаний в точке местоположения m₁.

                                                                                

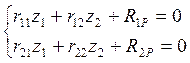
Определим коэффициенты канонического уравнения.

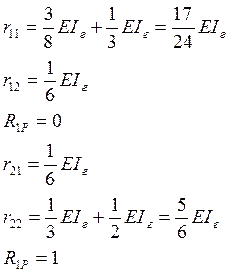
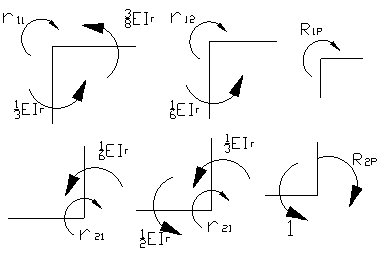
Решаем кананическое уравнение:

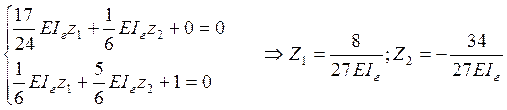
Строим исправленные эпюры.

 

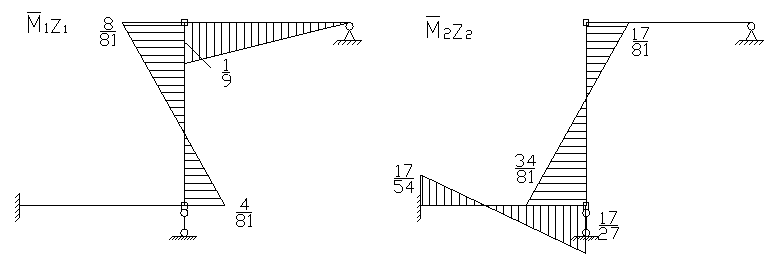
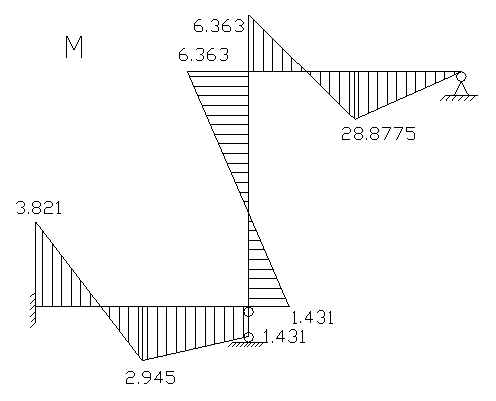
Строим эпюру моментов:

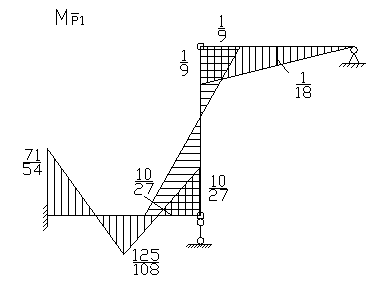
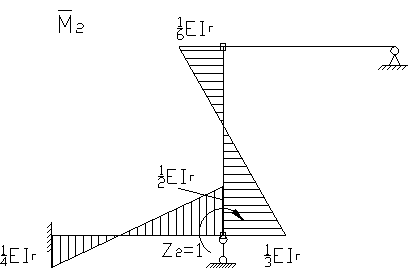
2.2 Для определения коэффициентов векового уравнения построим эпюру моментов в заданной системе от силы  приложенной в направлении возможных колебаний в точке местоположения m₂.

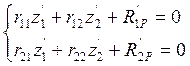
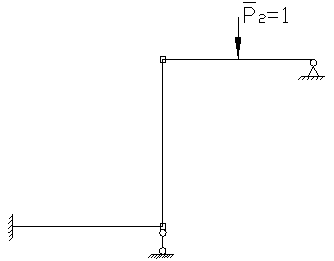
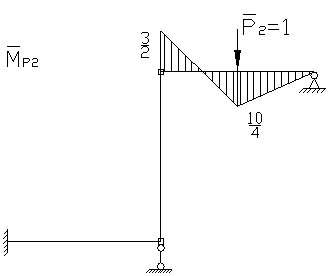
Определим коэффициенты канонического уравнения.

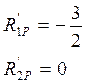
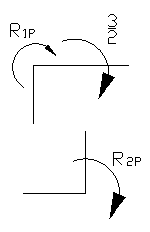
Решаем кананическое уравнение:

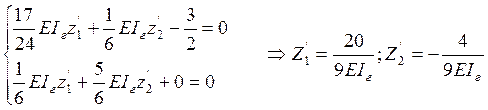
Строим исправленные эпюры.

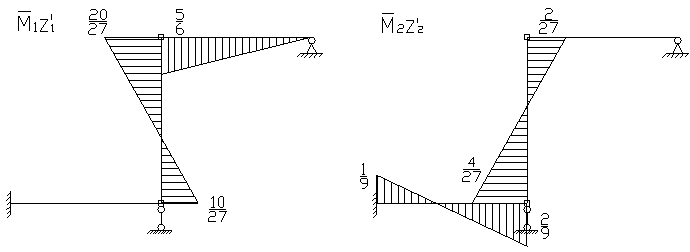
Строим эпюру моментов:

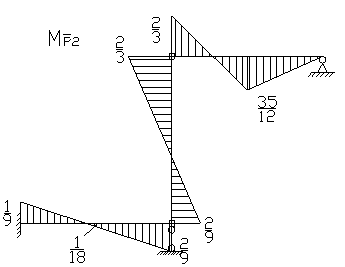
Определим коэффициенты векового уравнения:

 

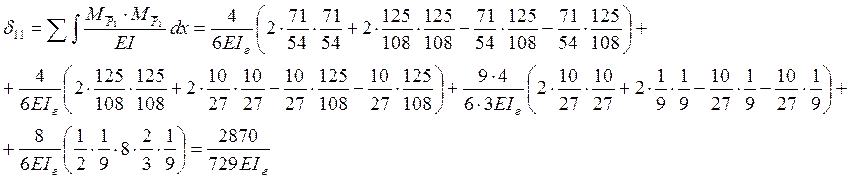
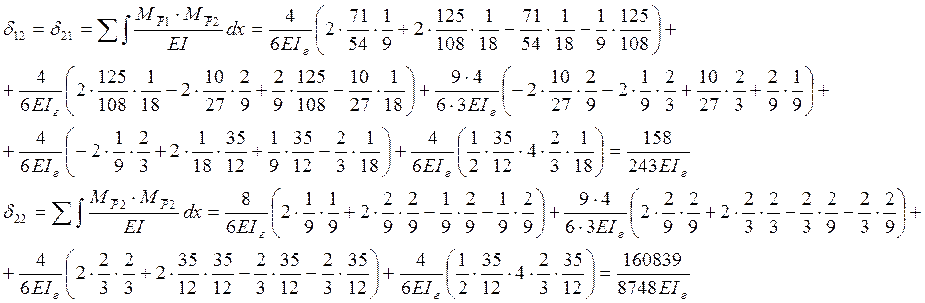
Решаем вековое уравнение:

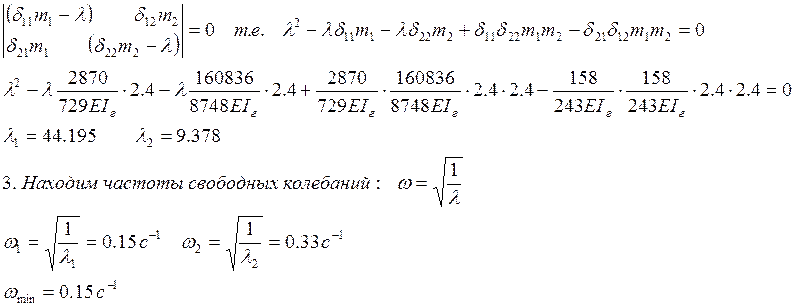4.Определяем частоту вынужденных колебаний системы.

                          

5.Определяем значение изгибающих моментов от амплитудного воздействия заданных вибрационных сил.

Составим уравнение для определения сил инерции.

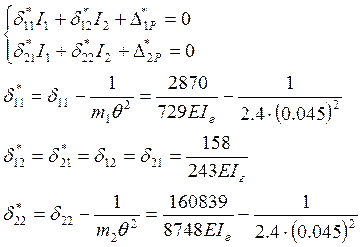
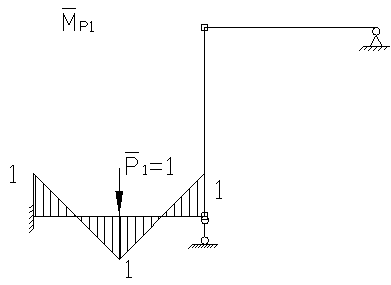
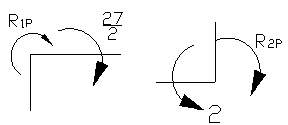
Для определения  необходимо построить эпюру моментов в заданной системе от амплитудного значения заданных вибрационных нагрузок.

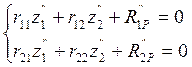
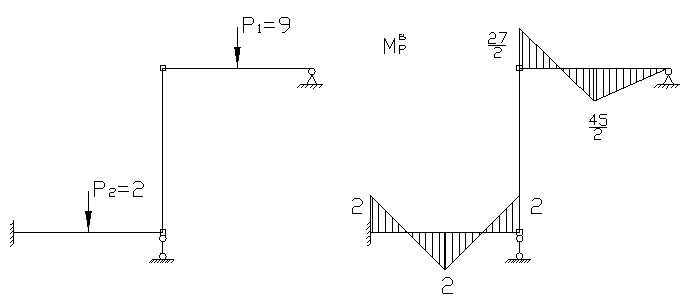
Определим коэффициенты канонического уравнения.

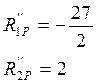
Решаем кананическое уравнение:

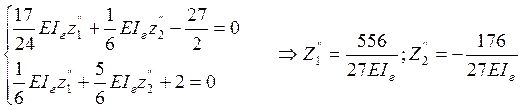
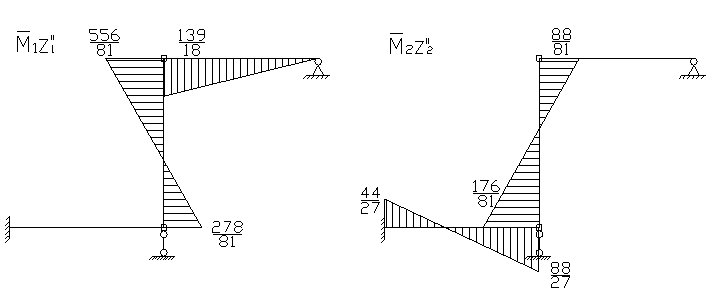
Строим исправленные эпюры.

Строим эпюру моментов:

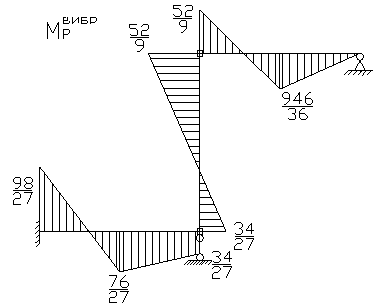
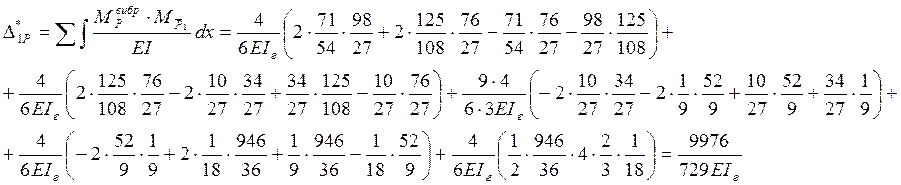
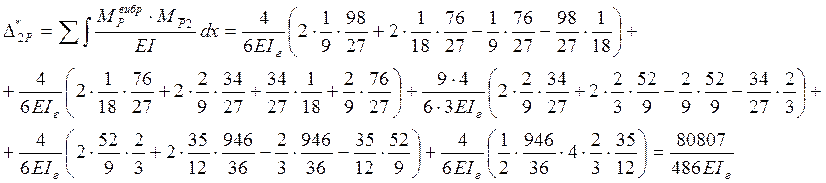
Определим силы инерции.

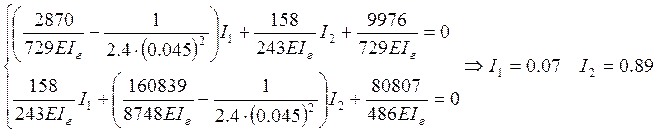
Строим окончательные эпюры от воздействия инерционных сил.

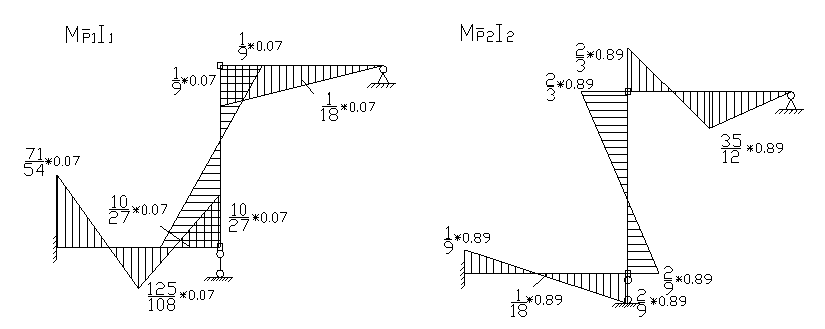
Строим эпюру от динамического воздействия вибрационных сил и сил инерции.