Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики
Кафедра Систем Управления и Информатики
Лабораторная работа № 4
"Идентификация сигналов по текущим наблюдениям"
по курсу "Идентификация и диагностика систем
|
Выполнил: |
Студенты гр. 4146
|
|
Преподаватель: |
|
Санкт-Петербург
2007 г.
Цель работы: исследование задачи идентификации сигналов, наблюдаемых в присутствии аддитивных ошибок измерений, рекуррентным методом наименьших квадратов.
Пусть s(t) – выборочная функция некоторой совокупности.
Измерения сигнала s(t) производится в дискретные моменты времени и сопровождаются аддитивными ошибками наблюдения ν(t), так что доступный наблюдению сигнал равен
z(t)=s(t)+ ν(t), t=0,1,2,3…
Ошибки наблюдения ν(t) представляют собой последовательность независимых случайных величин с нулевым средним и ограниченным вторым моментом:
![]()
Отсутствие априорной информации о вероятностных характеристиках сигнала s(t) и ошибках наблюдения делает невозможным использование результатов теории оптимальной калмановской фильтрации и приводит к необходимости построения модели сигнала s(t) в виде линейной комбинации конечного набора линейно-независимых функций из заданного класса:
![]()
так что уравнения наблюдения имеют вид:
![]()
t=1,2,…,i, где uj(t), j=1(1)n – функции выбранной базисной системы; θj, j=1(1)n – параметры модели сигнала; ν(t) – ошибки измерения.
Схема моделирования:
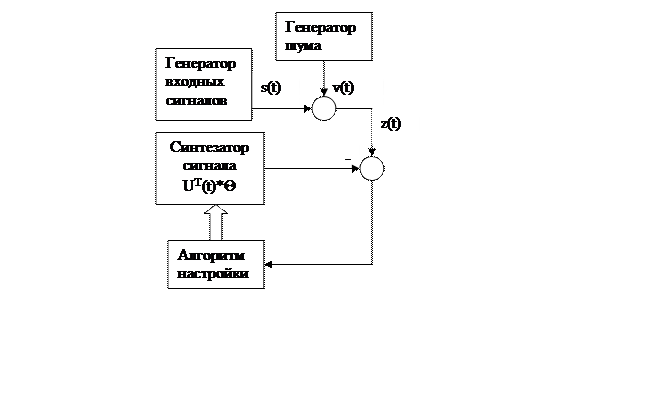
1. Функция вида:
![]()
Параметры:
a=3
b=0.85
c=0.008
Порядок полинома:
n=1
Помеха: отсутствует.
Дисперсия помехи:
Результаты вычислений:
![]() qi=[0.079728, -0.00070266]
qi=[0.079728, -0.00070266]
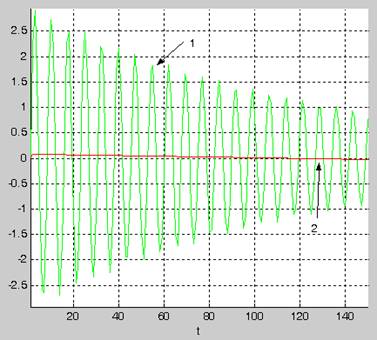
1- график идентифицируемого сигнала
2- график синтезированной по текущим наблюдениям модели сигнала
Помеха: присутствует
Дисперсия помехи: 0,3
Результаты вычислений:
![]() qi=[-0,082663, 0.0010342]
qi=[-0,082663, 0.0010342]
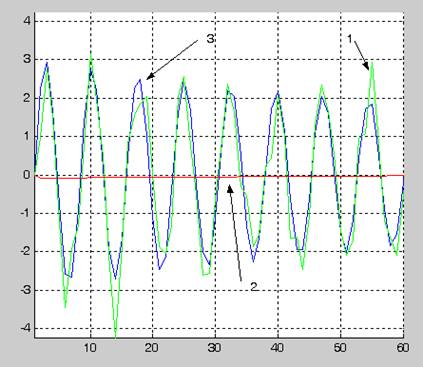
3- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
1- график смеси сигнала и ошибок наблюдения
2. Параметры:
a=8
b=0.85
c=0.008
Порядок полинома:
n=1
Помеха: отсутствует.
Дисперсия помехи:
Результаты вычислений:
![]() qi=[0.26261, -0.0018738]
qi=[0.26261, -0.0018738]
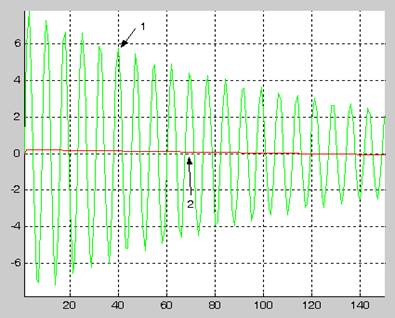
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
Помеха: присутствует
Дисперсия помехи: 0,3
Результаты вычислений:
qi=[0,050217, -0.00013689]
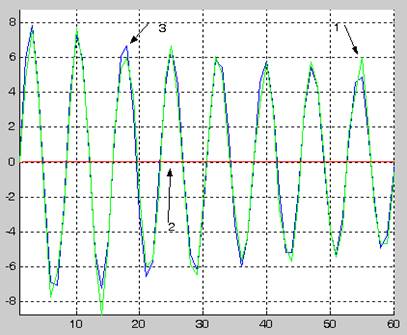
3- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
1- график смеси сигнала и ошибок наблюдения
Вывод: при увеличении параметра а, графики сигнала и смеси сигнала и ошибок практически идентичны, что говорит о том что с ростом а уменьшается влияние ошибок на график сигнала.
3. Параметры:
a=3
b=3
c=0.008
Порядок полинома:
n=1
Помеха: отсутствует.
Дисперсия помехи:
Результаты вычислений:
![]() qi=[0.0066942, -0.00010436]
qi=[0.0066942, -0.00010436]
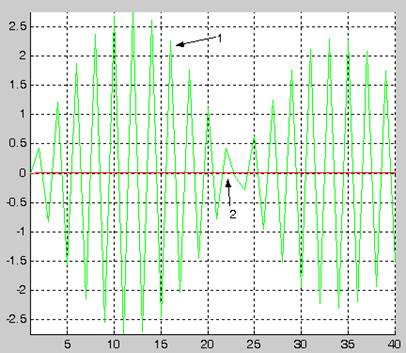
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
Помеха: присутствует
Дисперсия помехи: 0,3
Результаты вычислений:
qi=[-0,1557, 0.0016325]
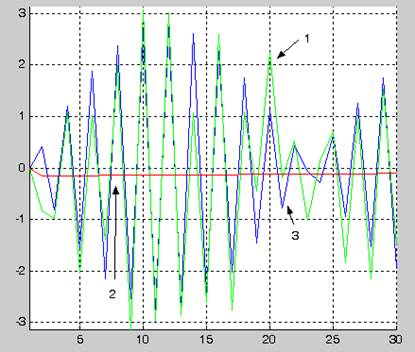
3- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
1- график смеси сигнала и ошибок наблюдения
Вывод: при увеличении параметра b, увеличивается частота сигнала, но влияние ошибок значительно.
4. Параметры:
a=3
b=0,85
c=0.05
Порядок полинома:
n=1
Помеха: отсутствует.
Дисперсия помехи:
Результаты вычислений:
![]() qi=[0.088798, -0.00088445]
qi=[0.088798, -0.00088445]
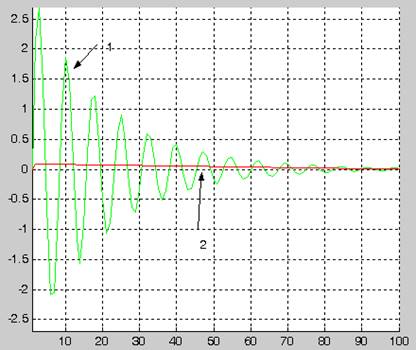
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
Помеха: присутствует
Дисперсия помехи: 0,3
Результаты вычислений:
qi=[-0,073593, 0.00085241]
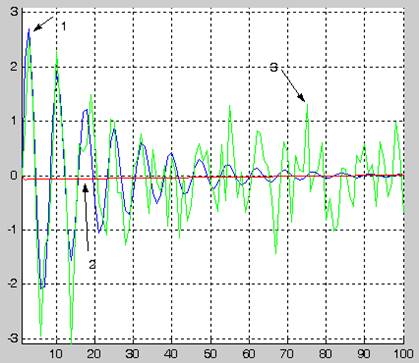
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
3- график смеси сигнала и ошибок наблюдения
Вывод: при увеличении параметра b, уменьшается время сходимости алгоритма, но влияние ошибок значительно
5 Параметры:
a=3
b=0.85
c=0.008
Порядок полинома:
n=1
Помеха: присутствует
Дисперсия помехи: 1,3
Результаты вычислений:
qi=[-0,25832, 0.0029129]
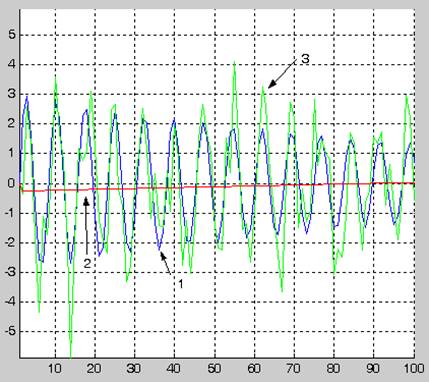
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
3- график смеси сигнала и ошибок наблюдения
Вывод: при увеличении дисперсии помехи, увеличивается влияние ошибок. График смеси сигнала и ошибки значительно отличается от графика идентифицируемого сигнала.
6 Параметры:
a=3
b=0.85
c=0.008
Порядок полинома:
n=5
Помеха: отсутствует.
Дисперсия помехи:
Результаты вычислений:
![]() qi=[0.84273, -0.093229, 0.0031474, -4,4816*10^5,
2.8336*10^-7, -6,5609*10^-10]
qi=[0.84273, -0.093229, 0.0031474, -4,4816*10^5,
2.8336*10^-7, -6,5609*10^-10]
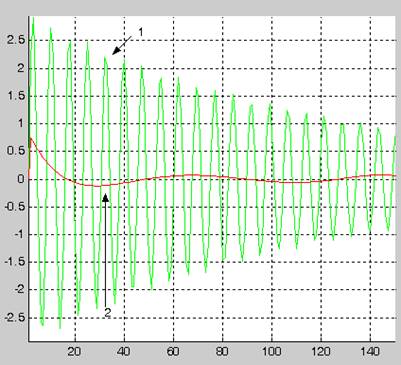
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
Помеха: присутствует
Дисперсия помехи: 0,3
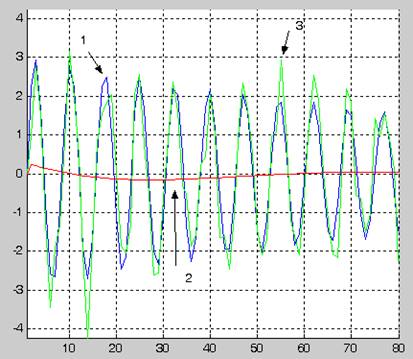
1- график идентифицируемого сигнала
2-график синтезированной по текущим наблюдениям модели сигнала
3- график смеси сигнала и ошибок наблюдения
Вывод: при увеличении порядка полинома изменяется график синтезированной по текущим наблюдениям модели сигнала, но никак не влияет на идентифицируемый сигнал и ошибки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.