Вариант № 1.
Вставить:
|
 |
|
|||
Для достижения гибкости и универсальности роботов-манипуляторов их кинематические схемы должны иметь дополнительные степени свободы. Избыточные многозвенные роботы способны выполнять нетривиальные задачи перемещения, такие, как проникновения в труднодоступные области рабочей зоны, обход препятствий, приближение к удаленным объектам, движение вдоль сложных криволинейных траекторий и т.д. Решение этих задач, а также эффективное использование дополнительных степеней свободы в процессе движения робота порождает определенные трудности управления, известные как проблема избыточности.
Нарисовать:
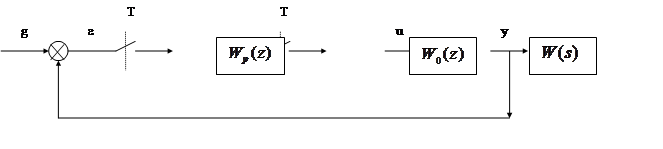 |
Вариант № 2.
 |
Вставить:
|
||||
![]()
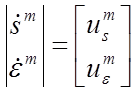 |
|||||
|
|||||
Эти трудности
вызваны неопределенностью конфигурации робота, а также необходимых управляющих
воздействий, когда число управляемых степеней свободы больше, чем число измерений
Декартова пространства. Наиболее сложные задачи управления связаны с
пространственным движением гиперизбыточных роботов (сочлененных и змееподобных
роботов, ферм с изменяемой геометрией). Наиболее естественный путь разрешения
неопределенности управления избыточным роботом состоит во введении
дополнительных ограничений движения робота. Эти ограничения, записываемые как
голономные зависимости переменных робота ![]() ,
могут определять, например, условия идентичности или пропорциональности
координат и их скоростей, желаемой ориентации звена в декартовом пространстве.
Наиболее наглядно зависимости декартовых координат представлены аналитическим
описанием траектории конечной точки или траекторий других важных точек
кинематической цепи робота.
,
могут определять, например, условия идентичности или пропорциональности
координат и их скоростей, желаемой ориентации звена в декартовом пространстве.
Наиболее наглядно зависимости декартовых координат представлены аналитическим
описанием траектории конечной точки или траекторий других важных точек
кинематической цепи робота.
Нарисовать:
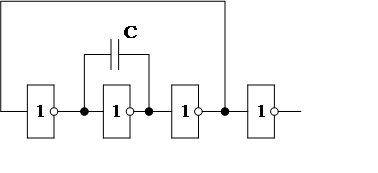 |
Вариант № 3.
Вставить:
|
Direct kinematics
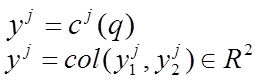 |
|
Nonlinear relations of outputs (m-1 coordination conditions)¯
Выполнение дополнительных ограничений обеспечивает согласованное движение звеньев избыточного механизма и сохранение его желаемой конфигурации в процессе движения конечной точки по заданной траектории. Такое поведение робота может быть получено методами программного управления, когда согласующие зависимости используются в процессе вычисления обратной кинематики. Тем не менее, стратегия следящего управления имеет определенные недостатки, выраженные в сложности оперативного вычисления обратной кинематики и точной интерполяции желаемых траекторий, а так же в сниженном динамическом качестве отслеживания задачно-ориентированных координат. Для гиперизбыточных роботов были предложены методы решения с использованием концепции «бесконечного числа степеней свободы», что не так эффективно в случае, если число звеньев робота не очень велико.
Нарисовать:
|
|
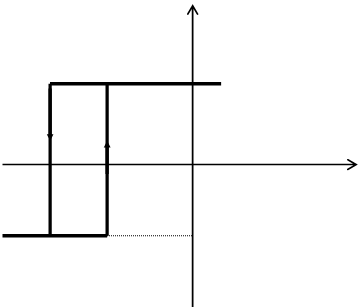 |
|
|
|
|
|
|
|
|
|
|
|
Вариант № 4.
Task-oriented variables:
Вставить:
|
Transversal error (orthogonal deviation of end-point)
|
![]() Nominal Jacobian matrix
Nominal Jacobian matrix
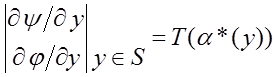 |
Прямое решение задачи управления робота с голономными ограничениями, основанное на принципе согласованного управления [3], дано в [7-8]. Оно подразумевает введение необходимого числа задачно-ориентированных координат
![]()
характеризующих отклонения от желаемых ограничивающих зависимостей. Таким образом, многомерная задача управления сводится к множеству простых задач стабилизации, решаемых с помощью методов нелинейного управления [3,8-9].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.