System transformation. Model in Cartesian space. Task-oriented model for the end link. Task-oriented model for intermediate pointsÝ, страница 2

Нарисовать:

 

Вариант № 5.

(i) orthogonal matrix (Frenet frame)Ñ

Вставить:

 

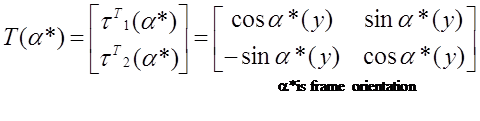(ii) Frenet-like equation

			x=x(y) is a curvature
					Figure 5

 

Данная статья обсуждает задачу траекторного движения для двух типов плоских избыточных манипуляторов. Для того, чтобы сохранять желаемую конфигурацию многозвенного робота, задача управления предполагает стабилизацию ведущих точек кинематической цепи робота по некоторой гладкой кривой (Декартовой траектории) в процессе их продольного движения. Решение основано на современных подходах теории нелинейного и многосвязного управления. Основные проблемы (связанные с избыточностью системы, согласованием движения звеньев робота и необходимостью обеспечить его компактную конфигурацию) сведены  к задачам согласования выходов и стабилизации нелинейной модели относительно пространственных (плоских) аттракторов. Полученная система включает нелинейные преобразования управляющих воздействий и набор простых регуляторов, обеспечивающих выполнение локальных задач стабилизации.

 

Нарисовать:

Вариант № 6.

2. МОДЕЛЬ РОБОТА И ОПРЕДЕЛЕНИЕ ЗАДАЧИÝ

В этом разделе рассматривается плоский многозвенный робот, состоящий из стандартных звеньев с одной степенью свободы. Кинематика j-го звена описывается уравнением

 

(1)

где  - вектор Декартовых координат ведущей (центральной) точки  и  - угол j-го звена,  - длина звена,  - ортогональная матрица ,

.

Легкий плоский робот со стандартными звеньями является пространственным кинематическим механизмом с m степенями свободы, описываемым уравнениями

(2)

(3)

где  - вектор обобщенных координат,  - вектор управляющих воздействий,

 

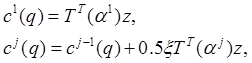(4)

j = 2,…,m, и

 

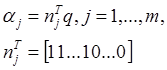(5)

Вставить:

 

Нарисовать:

Вариант № 7.

2. МОДЕЛЬ РОБОТА И ОПРЕДЕЛЕНИЕ ЗАДАЧИß

Дифференцируя уравнение (3) по времени и подставляя (2), получаем модель робота в Декартовом пространстве

 

(6)

где матрицы  вычисляются как

 

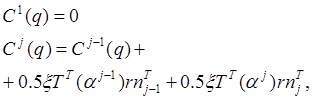(7)

j = 2,…m,

Рассмотрим движение робота в Декартовом пространстве Y по некоторой гладкой кривой , заданной уравнением

 

(8)

полагая, что длина пути определена как

 

(9)

Далее мы будем использовать ортонормированное описание кривой (см. [3]), для которого гладкие функции  и  принимаются такими, что матрица Якоби

отображения  на кривой  является ортогональной, или

 

(10)

 

Нарисовать:

Вариант № 8.

2.3. В двоичном канале со стиранием используется код (7,4) с образующей матрицей

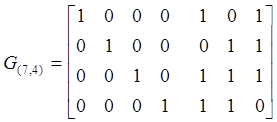
при передаче кодовой комбинации 1011100 принятая комбинация имеет вид 10*11*0, где символ * принадлежит зоне стирания. Исправимы ли произошедшие стирания?

3.   Цифровая и аналоговая схемотехника¡

3.1. Составить схему на операционных усилителях, реализующую статическую характеристику

Нарисовать:

 

	0

 

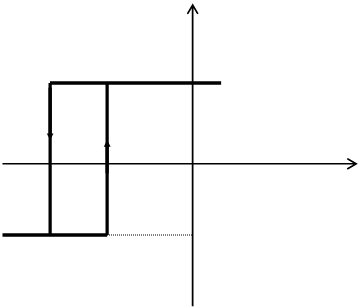3.2. Привести временные диаграммы на выходе следующей схемы

Нарисовать:

 

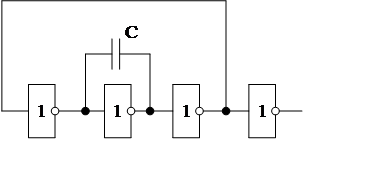Вариант № 9.

МОДЕЛЬ УПРАВЛЕНИЯâ

Определим нарушения условий (12), связанные с ортогональными отклонениями от кривой , с помощью переменных

 

(15)

Уравнения (13) и (15) представляют изменения координат (преобразование задачно-ориентированных переменных робота [3]). Задача управления сводится к (асимптотической) компенсации отклонений  и поддержанию зависимости (14).

Для получения задачно-ориентированной модели продифференцируем уравнения (13), (15) и, после замены (6), найдем

 

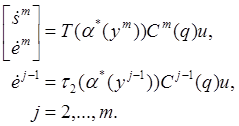(16)

Теперь преобразуем переменные согласно выражениям

 

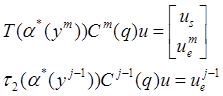(17)

(18)

где - продольное, а  - поперечные управляющие воздействия. Тогда уравнения (16) принимают вид

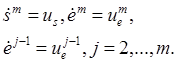(19)

(20)

		g		e		y

 

Нарисовать:

---