Государственный комитет РФ по рыболовству.
Мурманский государственный технический университет.
Расчетно-графическое задание по статистике
г Мурманск
2000
БЛОК I "ОБЩЯЯ ТЕОРИЯ СТАТИСТИКИ"
ЗАДАЧА № 1
По данным о поквартальном товарообороте предприятия в 1998 году:
|
Показатели |
Квартал 1998 г. |
|||
|
I |
II |
III |
IV |
|
|
Объем товарооборота (тыс. руб.) |
530 |
500 |
640 |
700 |
проведите согласование ряда и сделайте прогноз на первый квартал 1999 г. Рассчитать темп роста товарооборота и средний темп роста за последние три квартала. Сделайте выводы.
1.Рассчитаем абсолютные цепные приросты:
Dyi = yi - yi-1
Dyi1 = 500 – 530 = -30 (т.р.)
Dyi2 = 640 – 500 = 140 (т.р.)
Dyi3 = 700 – 640 = 60 (т.р.)
![]()
3.Прогноз на первый квартал 1999 года:
Объем товарооборота = 56,667 + 700 = 756,667тыс. рублей
|
|
4.Рассчитаем темпы роста:
|
|
|
|
|
|
За 1998 год в каждом квартале происходит среднее абсолютное изменение , объем товарооборота повысился на 56,667 тыс. рублей. В соответствии с этим можно сделать прогноз на первый квартал 1999 года и объем товарооборота составит 756667 рублей
Темп роста объема товарооборота во втором квартале по сравнению с первым кварталом составил 94%, то есть произошло понижение на 6%, в третьем квартале по сравнению со вторым темп роста составил 128%, то есть увеличился на 28%, в четвертом квартале по сравнению с третьим кварталом темп роста составил 109%, то есть увеличился на 9%. Средний темп роста за последние три квартала составил 118%, то есть увеличился на 18%.
ЗАДАЧА № 2
Проведено обследование 100 предприятий, характеризующихся сокращением производства. По приведенному интервальному вариационному ряду:
|
xi |
20£x1£30 |
30<x2£40 |
40<x3£50 |
50<x4£60 |
60<x5£70 |
|
Mi |
M1=5 |
m2=8 |
m3=4 |
m4=11 |
m5=2 |
1) Поясните, что является признаком, а что частотой его встречаемости (в соответствии с этим усовершенствуйте макет таблицы);
2) Рассчитайте средние (арифметическую, квадратическую, гармоническую), медиану и модальное значение признака, а также показатели вариации.
Сделайте выводы.
1.Так как дан интервальный вариационный , то в его основе лежит непрерывный признак, значение которого изменяется от 20 до 70 , то есть xi – признак, а mi - частота встречаемости признака, то есть это числа, которые показывают как часто встречаются те или иные варианты в ряду распределения.
Трансформируем таблицу и рассчитываем необходимые показатели:
|
П/н |
xi |
mi(fi) |
накопленная частота |
xi среднее |
xi*fi |
|
1 |
20-30 |
5 |
5 |
25 |
125 |
|
2 |
30-40 |
8 |
13 |
35 |
280 |
|
3 |
40-50 |
4 |
17 |
45 |
180 |
|
4 |
50-60 |
11 |
28 |
55 |
605 |
|
5 |
60-70 |
2 |
30 |
65 |
130 |
|
итого |
30 |
1320 |
1. Средняя арифметическая:
 |
|
|
|
|
2. Средняя квадратическая:
|
|
|
|
|
|
3. Медиана:
|
|
|
|
4. Мода:
|
|
Показатели вариации:
|
Группы xi |
расчетные показатели |
|||||||
|
mi |
xi сред знач |
xi*mi |
/xi-x/ |
/xi-x/*mi |
(xi-x)2 |
(xi-x)2fi |
||
|
20-30 |
5 |
25 |
125 |
-19 |
-95 |
361 |
1805 |
|
|
30-40 |
8 |
35 |
280 |
-9 |
-72 |
81 |
648 |
|
|
40-50 |
4 |
45 |
180 |
1 |
4 |
1 |
4 |
|
|
50-60 |
11 |
55 |
605 |
11 |
121 |
121 |
1331 |
|
|
60-70 |
2 |
65 |
130 |
21 |
42 |
441 |
882 |
|
|
Итого |
30 |
-------- |
1320 |
-------- |
334 |
1005 |
4670 |
|
|
Абсолютные |
Относительные |
|
R=64 - 25=40 размах вариации |
коэффициент вариации |
|
|
|
|
|
|
|
|
|
Вывод:
Для характеристики колебаемости признака используют ряд показателей. Наиболее простой из них R, который равен 40. Но этот показатель улавливает только крайние отклонения и не отражает отклонения вариант в ряду. Чтобы дать обобщающую характеристику вычисляют отклонение , который равен 11,133. Таково в среднем варианты признака от их средней величины. Но отклонение по сравнению со средней величиной признака очень большое, оно отличается от среднего на 32,867. Это свидетельствует о том, что данные совокупности в отношении нашего признака неоднородны, а средняя нетипична. На практике меру вариации наиболее объективно отражает показатель дисперсии , который равен 155,6667, а средне квадратическое отклонение измеряет силу воздействия прочих факторов и составляет 12,48. Коэффициент вариации является наиболее распространенным показателем колебаемости, используемым для оценки средних величин , он составляет 28,36, так как Vσ < 33%, то можно сказать, что наша совокупность является однородной. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины. Коэффициент осцилляции отражает относительную колебаемость крайних значений признака вокруг средней.
ЗАДАЧА № 3
На фирме, состоящей из трех подразделений, проводится исследование по стажу работы. Результаты обследований приведены в таблице
|
Стаж работы (лет) |
До 5 |
5 - 15 |
15 - 25 |
Свыше 25 |
|
№ подраздел. |
||||
|
I |
2 |
5 |
20 |
10 |
|
II |
10 |
20 |
10 |
15 |
|
III |
3 |
10 |
30 |
5 |
Оцените средний уровень стажа в каждом подразделении и по всей фирме в целом; проведите сравнение общего среднего стажа по подразделениям со средним стажем по фирме в целом. Сделайте выводы.
Так как дан интервальный ряд и его крайние границы открыты, то для решения задачи перейдем к моментному ряду.
Рассмотрим второй и третий интервал, их величины:
15–5 = 25-15 = 10.
10/2 = 5; для перехода к моментному ряду интервал справа будет выглядеть:
25+5 = 30, а слева 5-5 = 0.
|
Стаж работников |
0 |
10 |
20 |
30 |
всего |
|
№ подразделения |
|||||
|
1 |
2 |
5 |
20 |
10 |
37 |
|
2 |
10 |
20 |
10 |
15 |
55 |
|
3 |
3 |
10 |
30 |
5 |
48 |
|
Всего |
15 |
35 |
60 |
30 |
140 |
|
|
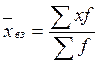 |
2.
|
|
3.
|
|
Средний уровень стажа по всем подразделениям:
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.