Точки и множества на плоскости и в пространстве. Комплексные числa. Многочлены и рациональные функции

Академия управления          при Президенте Республики Беларусь

 

Математика для менеджера

Практикум

 (Часть I)

Минск 2001

СОДЕРЖАНИЕ

Введение. 3

§ 1. Точки и множества на плоскости  и в пространстве. 6

§ 2. Комплексные числa. 9

§ 3. Многочлены и рациональные функции. 13

§ 4. Определители и матрицы.. 18

§ 5. Методы решения систем линейных уравнений. 28

§ 7. Прямая на плоскости. 33

§ 8. Плоскость. 37

§ 9. Кривые второго порядка. 41

§ 10. Преобразование координатной системы.. 48

§ 11. Последовательности. 53

§ 12. Функции. 60

Введение

Предлагаемый практикум завершает разработанный на кафедре Информационных технологий управления комплекс учебных пособий «Математика для менеджера».

Этот комплекс содержит:

-  лекционные материалы по курсу «Высшая математика» (части I и II);

-  методические рекомендации и контрольные работы с примерами для заочного математического образования менеджера-экономиста,

-   набор тестов для оценки знаний по курсу «Высшей математики»;

-  комплекс лабораторных работ по основам постановки задач менеджмента, их алгоритмизации, программирования и основным методам вычислительной математики для решения задач менеджмента (часть III), в том числе с применением математических пакетов Derive и Maple;

-  лекционные материалы и практикум по теории вероятностей и математической статистике (части IV и VI);

-  справочник и примеры постановки и решения задач экономики и менеджмента с использованием основных разделов курса «Высшей математики» (часть V).

Конечная цель части VII данного комплекса учебных пособий «Математика для менеджера» – освоение на алгоритмическом уровне на взаимосвязанных примерах возможностей практического применения аппарата отдельных разделов курса «Высшей математики». Последовательное применение практикума должно обеспечить формирование навыков использования математического аппарата и устойчивого алгоритмического и математического мышления у будущего менеджера-экономиста. Составители практикума исходили из того, что навыки математической и алгоритмической постановки экономико-управленческих задач ведут к успешному деловому взаимодействию менеджера-экономиста со специалистами по прикладной математике как основе современной технологии моделирования и решения задач стратегического  и оперативного менеджмента.

В этой связи данный практикум построен так, чтобы дать обучаемому краткие сведения по основным разделам курса, достаточные для выполнения операций над различными  математическими объектами и показать в комплексе взаимосвязанных задач для самостоятельного решения наиболее важные варианты выполнения операций математической технологии (рис. 1). Подбор комплекса задач и самостоятельных заданий, их решение, как надеются авторы, должны дать будущему менеджеру элементы  владения языком описания различных проблемных  ситуаций для взаимодействия с прикладными математиками.

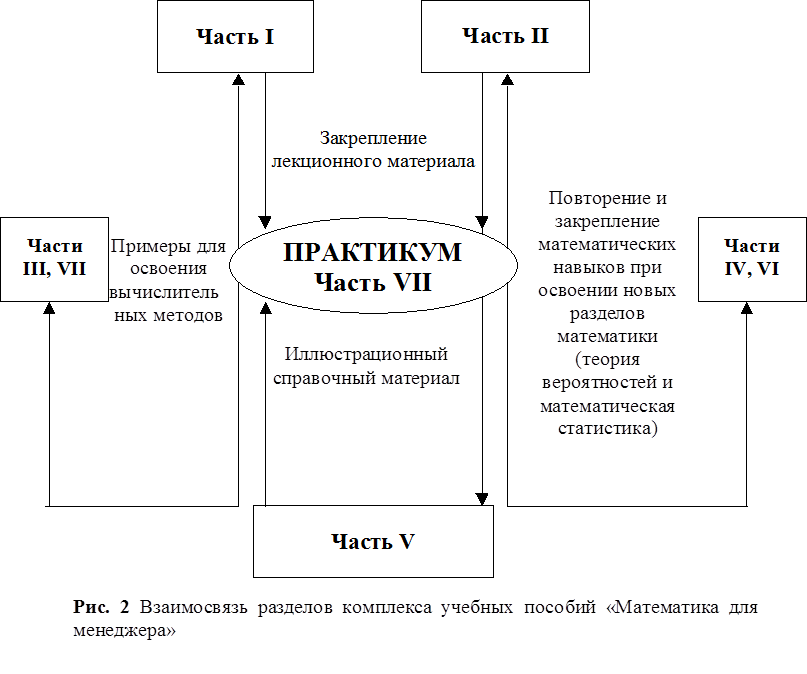
В процессе освоения практикума следует применять части I, II, V комплекса учебных пособий «Математика для менеджера» (рис. 2).

Завершив освоение любого из разделов данного практикума, следует проверить свою готовность к составлению алгоритма выполнения конкретных математических операций для конкретного упражнения или задачи. Успешное построение алгоритма может служить основанием для оценки степени освоения практикума.

§ 1. Точки и множества на плоскости и в пространстве

Задания для самостоятельного решения

1.  Изобразить на координатной плоскости точки:

2.  Изобразить на числовой прямой множества чисел , удовлетворяющих условиям:

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)
15)	16)
17)	18)
19)	20)
21)	22)

3.  Изобразить на координатной плоскости множества точек  удовлетворяющих условиям:

1)	2)
3)	4)
5)	6)
7)	8)
9)  .

4. Вычислить расстояние между точками  и , если:

1)	2)
3)	4)
5)	6)

5. Найти середину отрезка, если:

1)	2)	3)
4)	5)	6)
7)	8)	9)

6. В треугольнике  найти длины сторон, если:

1) 

2) 

7. Дан треугольник ,   Найти основания медиан.

8. В треугольнике  найти длины медиан, если:

1) 

2) 

9. Доказать, что треугольник с вершинами  равнобедренный. Будет ли он прямоугольным?

10. Доказать, что треугольник с вершинами  равнобедренный и прямоугольный.

11. На оси  найти точки, удаленные на расстояние 5 от точки  

12. Найти на плоскости  точки, удаленные на расстояние 5 от точек  и .

13. Найти координаты проекций точек

а) на координатные оси;

в) на координатные плоскости.

14. Треугольник  является проекцией треугольника  на плоскость  Найти длины сторон треугольника , если

§ 2. Комплексные числa

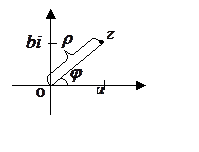Основные сведения

Комплексное число обычно записывают в алгебраической форме , где  а - действительная часть ,  - мнимая часть , R , или в тригонометрической форме

, где  - модуль  ;

  - аргумент  z,

,    .

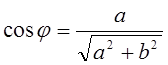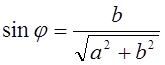Аргумент  определяется с точностью до . Главным значением аргумента будем считать  из промежутка . Общее значение  аргумента

.

При выполнении операций над комплексными числами можно использовать формулы Муавра. Если , то

;

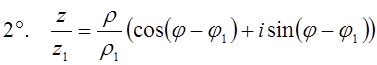,   если ;

.

Корень степени n из комплексного числа  имеет n различных значений, которые можно вычислить по формуле

Примеры решения задач

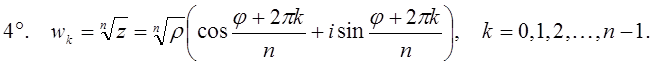
Пример 1. Вычислить .

Решение.  Представим число  в тригонометрической форме.

.

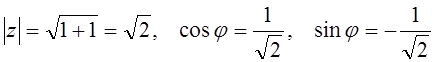Значит,  Поэтому .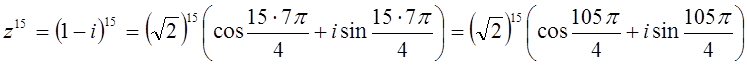

Пример 2.  Найти все значения .

Решение.  .

Воспользуемся формулой .

.

Задания для самостоятельного решения

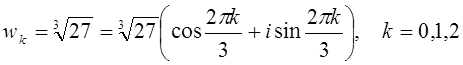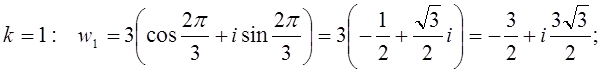
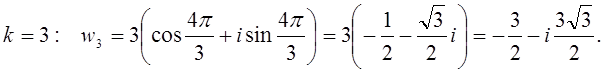
1. Вычислить

1)  ;	2)  ;
3)  ;	4)  ;
5)  ;	6)  ;
7)  ;	8)  ;
9)  ;	10)  .

2. Вычислить  если:

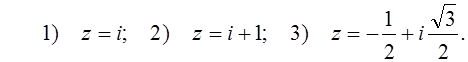
3. Изобразить на комплексной плоскости числа:

и сопряженные им числа.

4. Найти модуль и главное значение аргумента чисел:

и сопряженных им чисел.

5. Записать в тригонометрической форме числа:

6. Вычислить:

1)  ;	2)  ;
3)  ;	4)  .

7. Изобразить на комплексной плоскости множества точек , удовлетворяющих условию:

1)  ;	2)  ;	3)  ;
4)  ;	5)  ;	6)  ;
7)  ;	8)  ;	9)  ;
10)  ;	11)  ;	12)  .
13)	14)	15)  0 < Imz < 3.

8. Найти все значения корня:

1)  ;	2)  ;	3)  ;
4)  ;	5)  ;	6)  .

9. Решить уравнения:

1)  ;	2)  ;
3)  ; 5)  ;	4)  6)  ;
7)  ;	8)   .

§ 3. Многочлены и рациональные функции

Многочлены

Многочленом называют функцию вида

, где  - числа,   x - переменная. Обычно считают, что . Тогда  n - степень многочлена.

Пусть  имеет степень n,  - многочлен степени  m, причем . Тогда можно разделить  на  с остатком, т.е. представить  в виде .

Здесь  - частное (многочлен степени  n - m),  - остаток (многочлен, степень которого строго меньше m).

Деление можно выполнить "уголком".

Число a называют корнем многочлена , если . Корень a имеет кратность , если  делится без остатка на  и не делится без остатка на .

Многочлен с действительными коэффициентами может иметь комплексные корни. Если  - корень кратности , то  тоже корень кратности .

Многочлен с действительными коэффициентами можно представить в виде произведения неприводимых множителей.

(	, (1) г где    ,

 - степень многочлена .

Рациональные функции

Рациональная функция – отношение двух многочленов

.

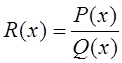Если степень  меньше, чем степень , то  называется правильной рациональной функцией.

Простейшими рациональными функциями называют функции вида