Производная и дифференциал. Правила Лопиталя. Экстремумы функций нескольких переменных. Определенный интеграл

Академия управления при Президенте Республики Беларусь

Математика для менеджера

Практикум

(Часть II)

Минск 2001

Содержание

§ 13. Непрерывность. 3

§ 14. Производная и дифференциал. 6

§ 15. Исследование функций. 16

§ 16. Правила Лопиталя. 25

§ 17. Формула Тейлора. 29

§ 18. Неопределенный интеграл. 35

§ 19. Определенный интеграл. 46

§ 20. Функции  переменных. 53

§ 21. Экстремумы функций нескольких переменных. 60

§ 22. Ряды.. 66

Литература. 80

§ 13. Непрерывность

Основные сведения  

Функция  называется непрерывной в точке , если

Это утверждение равносильно тому, что

Все основные элементарные функции непрерывны в любой точке, в которой они определены. Всякая арифметическая комбинация непре-рывных функций непрерывна в любой точке, в которой комбинация определена.

Композиция непрерывных функций непрерывна. Точнее: пусть . Если  непрерывна в точке , а  непрерывна в точке , то   непрерывна в .

Непрерывность функции  в точке , т.е. выполнение условия (1),  означает, что выполнены четыре условия, каждое их которых сильнее предыдущего:

1.   существуют;

2.   конечны;

3.  ;

4.  .

Если (1) не выполнено, то  называют точкой разрыва функции . Если при этом не выполняется условие 1., то  называют точкой неопределенности. Если 1. выполнено, но не выполнено условие 2., то  - точка бесконечного скачка. Если выполнены условия 1.,2., но не выполнено условие 3., то  называют точкой конечного скачка. Если выполнены условия 1.,2.,3., но не выполнено условие 4., то  называют точкой устранимого разрыва.

Точки устранимого разрыва и точки конечного скачка называют точками разрыва I рода. Точки неопределенности и точки бесконечного скачка называют точками разрыва II рода.

Если функция определена в окрестности точки  и не определена в самой точке , то такую точку также считают точкой разрыва.

Примеры решения задач

Пример 1.  Исследовать на непрерывность функцию .

Решение. Функция  является элементарной, она определена всюду в R, кроме . Значит, она непрерывна в любой точке . В силу того, что , точка   является точкой бесконечного скачка.

Пример 2.  Функция 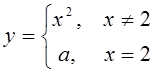  в точке  непрерывна как элементарная. При  имеем:   .  Если , то функ-ция непрерывна. Если , то  - точка устранимого разрыва.

Задания для самостоятельного решения

1. Доказать непрерывность функций в их области определения.

2.Определить функцию  в точке   так, чтобы функция стала непрерывной в этой точке.

3. Найти точки разрыва функции  и выяснить характер этих точек.

4. Изобразить схематично график функции вблизи точки разрыва в каждом из упражнений 3.

§ 14. Производная и дифференциал

Основные сведения

Функцию  называют дифференцируемой в точке , если ее приращение  в этой точке, вызванное приращением  переменной , представимо в виде

где  - число, зависящее от ,  при .

Число  называют производной функции  в точке . Ее обозначают

.

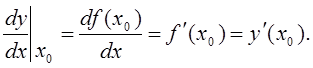
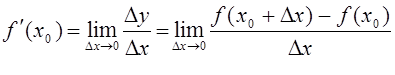Дифференцируемость функции в точке  означает, что в точке  существует касательная к графику функции. При этом число  является угловым коэффициентом касательной.

В формуле (1) величина  является главной частью приращения . Ее называют дифференциалом функции в точке  и обозначают . Если переменная   независимая, то   и, таким образом .

Таблица производных и дифференциалов основных элементарных функций

Правила дифференцирования

Производная сложной функции  (т.е. композиции ) вычисляется по правилу "цепочки"

.

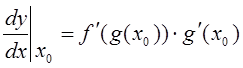Если  существует в каждой точке интервала , то  сама является функцией от . Производную этой функции называют второй производной или производной второго порядке функции  и обозначают .

Таким образом, . Аналогично определяют производные третьего порядка  и более высоких порядков . Принято считать . Если  и  - функции, имеющие производные порядка , то

;

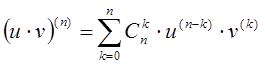 - формула Лейбница.

При вычислении производных старших порядков можно использовать формулы

.

В частности, если , то ;

;

;

;

.

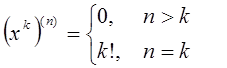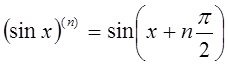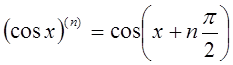Из формулы (1) следует что  или

Формулу (2) используют для приближенного вычисления значений функции.

Примеры решения задач

Пример 1. Пользуясь определением производной, найти производную функции  в точке .

Решение.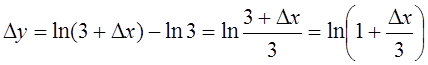

.

.

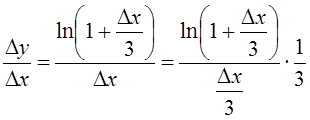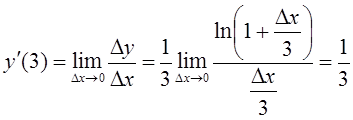Пример 2. Найти , если .

Решение. Последовательно вычисляем .

.

Воспользуемся формулой для .

.

Пример 3. Найти .

Решение. Воспользуемся формулой Лейбница, положив . Заметим, что  при .

Поэтому,

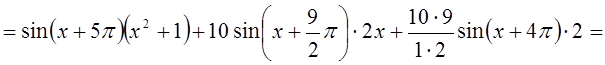
Пример 4. Вычислить приближенно .

Решение. Рассмотрим функцию .

При  получаем . Положим . Тогда . Воспользуемся формулой (2).

.

Применение производной в экономике

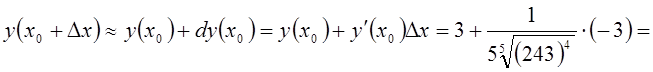
Рассмотрим производственную функцию , которая дает объем производимой продукции за единицу времени в зависимости от затрачиваемого ресурса . Как правило, производственные функция являются дифференцируемыми, таким образом, . В этом случае  - это добавочная продукция, произведенная за единицу времени за счет добавочного ресурса. Если принять за ресурс  количество человеко-часов, то  является продукция, производимая новым сотрудником предприятия за единицу времени. Если принять переменную  за цену единицы продукции, а переменную  - за зарплату работника в единицу времени, то при , можно сделать вывод, что нужно принять на работу еще одного работника, в силу того, что последний принесет прибыли фирме больше, чем фирма ему заплатит. В это и состоит золотое правило экономики. В рассматриваемой задаче  можно определить как предельную производительность труда.

Рассмотрим функцию ,  - приращение аргумента, а  - приращение функции. Тогда  и  - относительные изменения аргумента и функции соответственно