Общие сведения об электрических машинах. Электрическая машина, предназначенная для преобразования механической энергии в электрическую, страница 4

                                   (5-4)

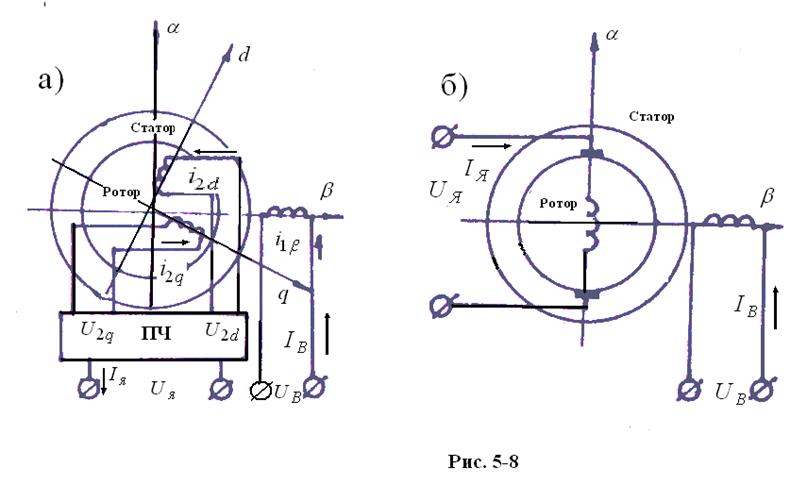
Обмотка статора  по оси  есть аналог обмотки возбуждения машины постоянного тока, а обмотки ротора по осям 2d и 2q - аналоги параллельных ветвей обмотки ротора машины постоянного тока.

Убедиться в справедливости (5-4) можно,  осуществив  приведение этих токов к неподвижным осям  и  :

,

Таким образом,  в осях   и  действительным переменным токам обмоток ротора двухфазной обобщенной машины  эквивалентен  ток  , протекающий по единственной роторной обмотке машины постоянного тока (по двум её параллельным ветвям) и создающий поле, неподвижное в пространстве и направленное вдоль оси  . 

          Интересно отметить,  что между частотой токов ротора и скоростью ротора существует однозначная связь,  которая не нарушается с изменением скорости ротора.  В этом отношении машина  постоянного  тока является синхронной, так как скорость вращения поля и скорость вращения ротора равны.

Для получения уравнений динамической механической характеристики воспользуемся уравнениями обобщенной электрической машины. В соответствии с рис.5-8 получим

  , 

     

 

После подстановки этих величин в (4-3), получим

                                            

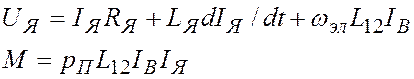
Заметим,      что               (5-5)                     

представляет собой выражение для э.д.с.  вращения  обмотки  ротора, где поток возбуждения, 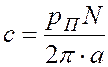- конструктивная постоянная, зависящая от числа пар полюсов "",  числа пар параллельных ветвей "а" и числа активных проводников обмотки ротора - ;

Уравнение для электромагнитного момента с учетом (5-5) принимает вид

5.3 Электромеханические свойства коллекторных двигателей постоянного тока независимого возбуждения

Двигатели постоянного тока имеют одно существенное преимущество - их движущие моменты зависят не от положения ротора и скорости вращения, а только от токов в обмотках якоря и возбуждения, т.к. конструкция машины обеспечивает ортогональность потока возбуждения и потока ротора. Если обмотки возбуждения заменить постоянными магнитами, то движущий  момент будет практически пропорционален току якоря, а скорость вращения  напряжению питания обмотки якоря. Двигатели с постоянными магнитами отличаются большим разнообразием, однако прежде чем рассматривать их основные конструкции и особенности, познакомимся с их общими свойствами.

Независимо от конструкции двигателя уравнения э.д.с. и электромагнитного момента имеют вид

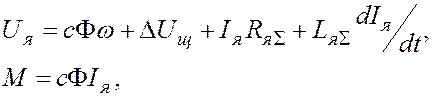                  (5-6)

где - напряжение и ток якоря;  - падение напряжения под щетками;   - индуктивность и сопротивление обмотки якоря;

Уравнение моментов:

                                    (5-7)

где  - результирующий момент инерции, равный сумме моментов инерции двигателя и приведенного момента инерции нагрузки;   Мс = Мо + Мн - момент сопротивления, равный сумме моментов холостого хода Мо и момента нагрузки Мн ;  М- электромагнитный момент двигателя.

Приведенные уравнения позволяют найти выражениедля механической характеристики двигателя:

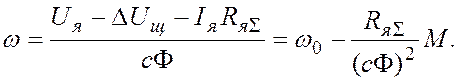                                             (5-8)   

и передаточные функции двигателя  по  управляющему  (напряжение  на якоре) и возмущающему (момент сопротивления) воздействиям:

 

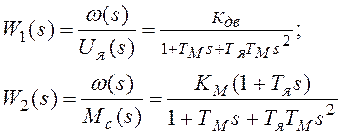
(5-9)

,                                         (5-10)

где - скорость идеального холостого хода; - коэффициент передачи двигателя; 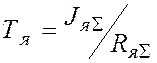 - электромагнитная постоянная якорной цепи; - электромеханическая постоянная времени;  ,   - индуктивность и сопротивление якорной цепи, которые кроме  содержат составляющие, определяемые цепями источника питания, сопротивлением щеточного контакта и дополнительными элементами, включенными в якорную цепь двигателя, в том числе соединительными проводами.

Приближенно падение напряжения под щетками можно учесть эквивалентным сопротивлением , тогда выражение для механической характеристики двигателя приникает вид                                                                           

              (5-11)

Из (5-11) следует, что механическая характеристика при  представляет собой прямую линию. Угловую скорость, соответствующую  М=0, равную при номинальном напряжении на якоре  , называют скоростью идеального холостого хода.