Электромеханические свойства асинхронных двигателей. Электромагнитная мощность, передаваемая через зазор ротору двигателя, страница 2

Э.д.с. ротора    определяет токи фаз обмотки ротора ,  при этом потребление энергии из сети возрастает,  что приводит и к возрастанию  тока статора.  Если все переменные цепи ротора привести к статору, то получим систему уравнений

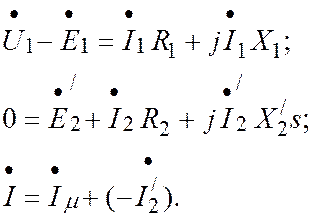                         (2)

В этой системе величины  и  - индуктивные сопротивления статора и ротора. Они определяются индуктивностями рассеяния соответствующих обмоток.  Можно считать,  что потоки рассеяния  и  , создаваемые обмотками статора и ротора,  совпадают по фазе с токами этих обмоток. Такое допущение справедливо, так как указанные потоки замыкаются главным образом по воздуху (поперек пазов, через коронки зубцов,  вокруг лобовых соединений). Поэтому можно считать, что для режимов  близких  к номинальному,  индуктивные сопротивления   и  не зависят  от  токов  соответствующих  обмоток.

Поскольку есть э.д.с.  рассеяния заторможенного ротора,  то при  вращении ротора э.д.с.  изменяется , а  индуктивное  сопротивление  вращающегося ротора имеет величину .

Система уравнений  (2)  позволяет  получить  схему   замещения  асинхронной машины, представленную на рис.4.

Полагая , из условия равенства мощностей приведенного и реального роторов   находим

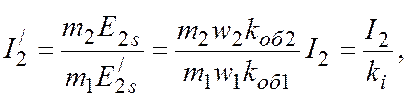
где - коэффициент приведения (трансформации) токов.

Из условия  равенства электрических потерь

получим            .

Из равенства  относительных индуктивных падений напряжений находим

.

Величину  называют коэффициентом приведения  сопротивлений. При определении коэффициентов приведения  и  для короткозамкнутой обмотки   ротора   типа "беличья клетка" принимают  , . Здесь - число проводников короткозамкнутой   обмотки. Воспользовавшись упрощенной схемой замещения асинхронного двигателя ( рис. 4), легко найти зависимости, определяющие его электромеханические свойства. Ток фазы ротора

, где   -  реактивное  сопротивление  короткого  замыкания (при S=1).

Электромагнитная мощность,  передаваемая через зазор ротору двигателя,

.                           (3)

Та же мощность может быть выражена через электромагнитный момент и скорость поля:

.                                                    (4)

Приравнивая (3) и (4), получим выражение для статической механической характеристики двигателя. При m = 3

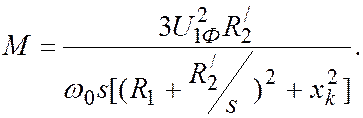                     (5)

  Характеристики   асинхронной   машины   могут быть легко получены  из анализа      обобщенной  электрической   машины.

На рис.5 представлена   двухфазная   модель асинхронного  двигателя с фазным ротором, эквивалентная схема двухфазной обобщенной электрической машины.  Математическое описание  в  неподвижных  осях     и  можно получить  из  уравнений  обобщенной машины,  положив  и обозначив штрихами приведенные к статору токи и  сопротивления  роторной цепи: 

                          (6)    где                                        

В установившемся режиме переменные двигателя представляют  собой синусоидальные величины,  изменяющиеся в осях   с частотой сети  .  Их можно представить в виде вращающихся векторов   и  т.д.

Поскольку сдвиг между осями   и   составляет 90  градусов  можно записать:

       

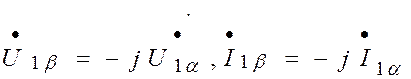
и т.д.   Учитывая, что

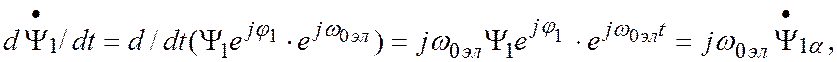
уравнения электрического равновесия для фазы   статора и ротора  из (6) могут быть представлены в виде

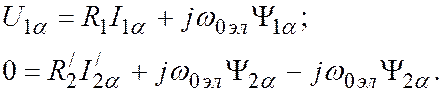                    (7)                   

Если  потокосцепления  машины выразить через намагничивающий ток , получим                    

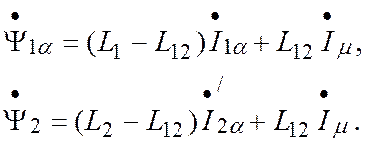
Параметры  двухфазной модели двигателя можно выразить через параметры трехфазного двигателя

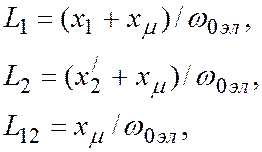
тогда уравнения (7) примут вид                                           

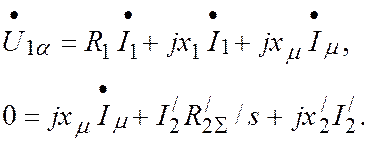                               (8)

Учитывая,  что  уравнения  (8)  совпадают  с (7), что говорит об эквивалентности рассматриваемых моделей.

Электромеханические свойства и характеристики асинхронного двигателя

Формула   (5)         определяет вид механической характеристики асинхронного двигателя, показанной на рис.6.

Эта характеристика имеет два максимума, которые могут быть найдены из уравнения . Максимумы данной характеристики  получили название критических точек.  Координаты критических точек  определяются зависимостями              

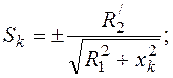                                        (9)

,                         (10)

причем отрицательное значение скольжения относится к генераторному режиму работы  машины, в этом режиме значение критического момента несколько выше, чем в двигательном.  Для двигателей различных серий величина критического момента в двигательном режиме, определяющая его перегрузочную способность по моменту  , лежит в пределах    1,7<< 3,6. Критический момент зависит от квадрата напряжения питания, поэтому асинхронные двигатели весьма чувствительны к колебаниям напряжения сети.