Математическое описание асинхронного двигателя при частотном управлении. Вектор намагничивающего тока

                                                                                                     Лекция 14

Математическое описание асинхронного двигателя при  частотном управлении

Применяя трехфазно-двухфазное преобразование, короткозамкнутый асинхронный двигатель можно свести к обобщенной электрической машине. Воспользовавшись уравнениями (2.5), получим:

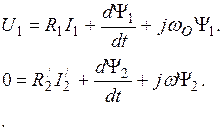                                           (2.17)

Недостатком этой математической модели является то, что уравнения записаны в разных системах координат.  Первое уравнение  в координатах  -, неподвижных относительно статора, а второе - в координатах    , неподвижных относительно ротора. Это затруднение можно преодолеть, записав оба уравнения в единой системе координат    неподвижной относительно магнитного поля статора  и вращающейся относительно обмоток статора со скоростью

Поскольку ротор вращается со скоростью   то относительно вращающейся системы координат его скорость будет равн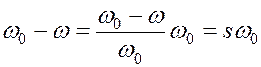а      .          Тогда                                           

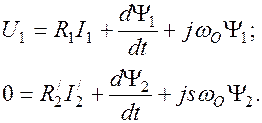                                (2.18)

В статическом режиме (2.18) принимает вид

  и                   (2.19)

Если выразить потокосцепления через токи, то из (2.19) получим выражение

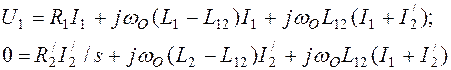,                (2.20)

где   вектор намагничивающего тока.

В уравнениях (2.20) целесообразно от индуктивностей перейти к индуктивным сопротивлениям, что позволит оценить изменение параметров асинхронного двигателя при изменении частоты.

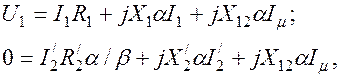                                              (2.21)

где относительная частота напряжения и тока статора;  абсолютное скольжение.  Системе уравнений (2.21) соответствует схема замещения, показанная на рис.2-3.

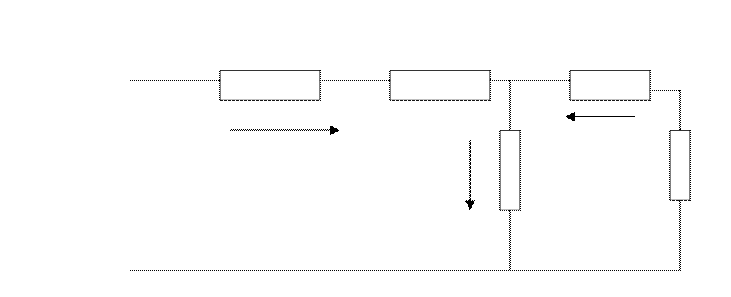
                                                                     Рис.2-3

Чтобы получить момент реального трехфазного асинхронного двигателя, выражение (2.12) надо умножить на 3/2 , позволит учесть различие  амплитуды изображающего  вектора и модуля переменных двухфазной обобщенной модели асинхронного двигателя.  Необходимо также  иметь в виду, что реальный асинхронный двигатель имеет   пар полюсов, поэтому скорость поля реального двигателя  равна     а не , как в обобщенной машине. В результате для трехфазного асинхронного двигателя  имеем

.                                 (2.22)

Если векторы потокосцепления и тока  представлены своими компонентами в ортогональной системе координат X-Y, вращающейся со скоростью поля и записаны в комплексной форме (действительная ось Х), то    

Следовательно, 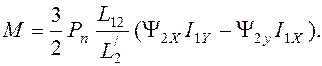                                   (2.23)

Как следует из (2.23) момент двигателя образуется взаимно перпендикулярными составляющими потока и тока.

3.Системы частотного управления асинхронными двигателями

Все многообразие систем частотного управления можно  условно разделить на   два  вида: скалярные и векторные.

3.1 Скалярные системы частотного управления

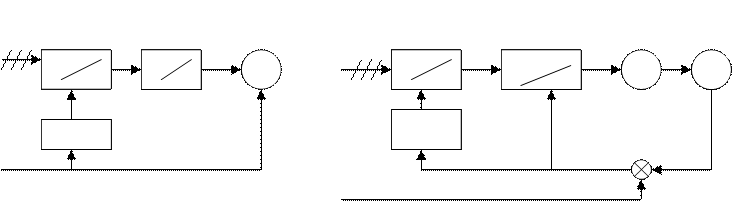
При скалярном управлении напряжение статора формируется в виде гармонического сигнала и система контролирует его действующее значение. При таком подходе регулируется только установившийся режим работы АД.  Частота напряжения статора и его амплитуда связаны между собой аналитической зависимостью  в соответствии с выбранным законом частотного управления.        При скалярном управлении различают независимое {а} и зависимое {б} управление частотой статора.

    =         =    АД                          =         =             АД       ДС

ЗН                                                       ЗН

                                                                                                                             +

                                                    +

                                     {а}                                                                                   {б}           

Рис.3-1

В первом случае сигнал задания   поступает от системы верхнего уровня, а в блоке ЗН происходит вычисление сигнала задания амплитуды  напряжения  в соответствии с выбранным законом частотного управления.