Симметричный оптимум. Системы подчиненного управления. Объект регулирования с одним интегрирующим звеном и многими звеньями с малыми постоянными времени

Лекция 10

СИММЕТРИЧНЫЙ ОПТИМУМ

В состав объекта управления могут входить не только инерционные звенья первого порядка, пропорциональные звенья и звенья с запаздыванием, но и интегральные звенья. В последнем случае компенсация наибольшей инерционности или двух самых больших инерционностей первого порядка уже не могут дать необходимого результата, т.к. интегральному характеру объекта управления противопоставляется интегральный характер регулятора. Это приводит к незатухающим синусоидальным колебаниям регулируемой величины.

Чтобы показать это, примем, что объект регулирования содержит интегрирующее звено и инерционное звено первого порядка с постоянной времени . Применим ПИ – регулятор, постоянная времени которого .

Передаточная функция разомкнутого контура регулирования будет иметь вид

.

Компенсация постоянной времени приводит к следующему результату:

.

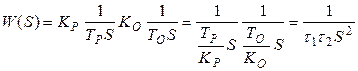Передаточная функция замкнутого контура  представляет собой передаточную функцию консервативного звена, которому соответствует незатухающий колебательный переходный процесс                       

.

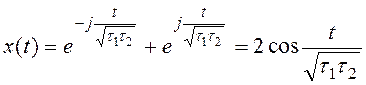Таким образом, оптимизацию контура регулирования с объектом, содержащим интегрирующее звено, необходимо осуществлять не по модульному оптимуму, а по иному принципу. Хотя и здесь следует добиваться  «пригонки» модуля передаточной функции к единице. Используя второе условие оптимизации , получим новое значение постоянной времени регулятора, которое приводит к получению логарифмической частотной характеристики симметричного вида. Вид ЛАХ дал название и способу настройки - настройка по симметричному оптимуму.

Объект регулирования с одним интегрирующим звеном и многими звеньями с малыми постоянными времени

Если объект регулирования содержит интегрирующее звено и некоторое число последовательно соединенных звеньев первого порядка, которые можно заменить эквивалентным звеном с суммарной постоянной времени, целесообразно применить ПИ –регулятор.

Уравнение передаточной функции разомкнутого контура

не дает возможности для компенсации, т.к. эквивалентная постоянная времени  принципиально не может быть скомпенсирована.

Передаточная функция замкнутого контура

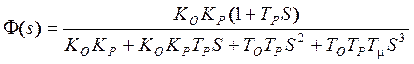
имеет в знаменателе полином, содержащий все сомножители от S⁰ до S³ . Следовательно, должна существовать возможность получения затухающего переходного процесса. Применим к этому уравнению второе условие оптимизации,  где , , , .

Окончательно получим ,  .

Эти значения, подставленные в уравнение передаточной функции, приводят к стандартному для симметричного оптимума уравнению

 .

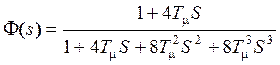Все контуры регулирования, настроенные на симметричный оптимум, имеют такой вид передаточной функции .

Поведение контура регулирования при этом виде оптимизации, также как и при модульной настройке, зависит только от суммы малых постоянных времени . Уравнение переходной характеристики имеет вид:      .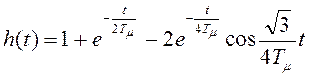

Из графика переходной функции контура регулирования видно, что время первого согласования равно , амплитуда первого перерегулирования    , а время переходного процесса .  

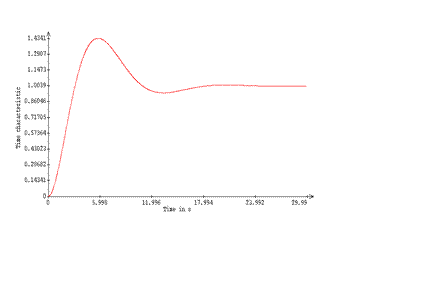
Рис.11   График переходной функции контура, настроенного на симметричный оптимум

Объект регулирования с интегрирующим звеном, одной большой и многими малыми инерционностями первого порядка

В этом случае необходимо применить ПИД-регулятор, причем время упреждения  должно быть равно постоянной времени .

Передаточная функция разомкнутого контура  имеет вид

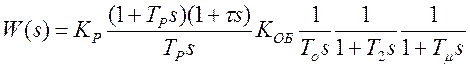, с учетом условия компенсации большой постоянной времени  получаем передаточную функцию, типичную для настройки на симметричный оптимум.

            Объект регулирования с инерционными звеньями первого порядка, одно из которых содержит постоянную времени превосходящую более чем в четыре раза сумму всех остальных постоянных времени:

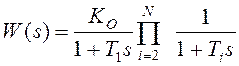                                          ,  где .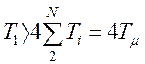

При таком соотношении параметров можно, используя ПИ – регулятор, настроить контур на симметричный оптимум, приняв , .

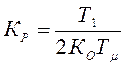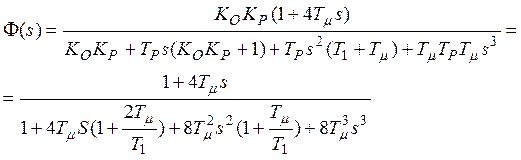
Уравнение лишь незначительно отличается от стандартного. Практически полное совпадение произойдёт, если  или .

Для симметрично оптимизированного контура с объектом состоящим только из инерционных звеньев 1-го порядка время первого согласования будет большим, а - меньшим, чем приведено на рис.8. В большинстве случаев здесь нет и отрицательной полуволны с  перерегулированием в 6%.

Отличие от переходной функции, присущей настройке на СО, и приближение к функции характерной для МО тем заметнее, чем ближе  приближается к единице. При

настройка соответствует настройке на модульный оптимум. Если применение правил настройки на симметричный оптимум теряет смысл, настройку контура следует вести на модульный оптимум.

Если в составе объекта есть не одно, а два звена с большими постоянными времени, предпочтение следует отдать ПИД -  регулятору. С помощью постоянной времени форсирующего (упреждающего) звена компенсируется вторая по величине постоянная времени.