Частотное управление асинхронными двигателями. Законы частотного регулирования. Регулирование с постоянной мощностью, страница 4

Динамика любой симметричной многофазной машины, имеющей m фаз статора и n фаз ротора, может быть путем замены переменных описана системой уравнений эквивалентной   двухфазной машины. Использование двухфазной модели двигателя позволяет избежать значительных вычислительных трудностей, связанных с увеличением числа уравнений и параметров машины, и за счет этого облегчить понимание природы преобразования энергии во вращающейся машине. При переходе от реальной трехфазной машины к ее двухфазной модели возникает  задача преобразования реальных переменных  Х_1А, Х_1В, Х_1С   к ортогональной системе координат  и , т.е. к реальным переменным двухфазной машины. Данная задача должна решаться отысканием формул преобразования переменных  при условии  инвариантности мощности. Представим реальные переменные в виде векторов и будем полагать, что преобразованные переменные в осях  и  пропорциональны сумме проекций  переменных Х_1А, Х_1В, Х_1С  на оси  и .

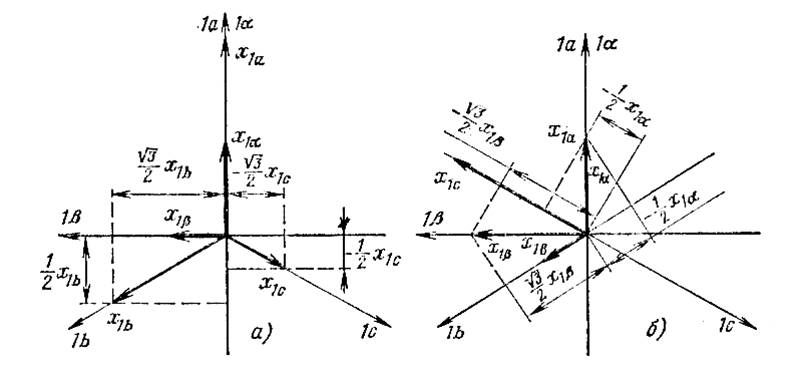
Рис.2-2

Из рис. 2-2 можно определить:                                                              

                                                                                                 

                     где К_С – согласующий коэффициент, выбор которого осуществляется из условия инвариантности мощности.

Для симметричной трехфазной машины выполняется условие

Х_1А +Х_1В+ Х_1С= 0,                                      (2-14)

поэтому (2.13) с учетом (2.14) преобразуется к виду

,

.                                     (2-15)

Переменные  Х_2d и Х_2q для роторной цепи также определяются по выражениям  (2.13) и (2.15) при соответствующей замене индексов.

Формулы обратного двухфазно-трехфазного преобразования можно получить  с помощью рис. 2-2, б:

,

                                        

(2.16)

При выполнении (2-14) третье уравнение системы (2-16) может быть получено из первых двух, т.к. .

Для определения согласующего коэффициента К_С, обеспечивающего выполнение условия инвариантности при преобразовании переменных, рассмотрим выражение для мгновенной мощности, потребляемой обмотками статора трехфазной машины из сети:

Из условия баланса мощностей исходного трехфазного двигателя и его двухфазной модели необходимо, чтобы согласующий коэффициент имел значение . При этом

 .

С четом согласующего коэффициента формулы трехфазно - двухфазного преобразования (2-13) приобретают вид

;                                                                             

,

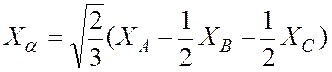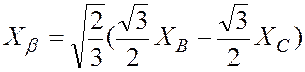Формулы (2.15) представляют собой трехфазно-двухфазное  преобразование, позволяющее реальный трехфазный асинхронный двигатель заменить эквивалентной системой двух ортогональных обмоток. Подставляя мгновенные значения переменных в (2.15)  получим

                                                         

Результирующий пространственный вектор  представляет собой векторную сумму потокосцеплений  и , т.е.

Модуль результирующего вектора ,  а аргумент -                   

В двухполюсной обобщенной машине  число пар полюсов равно единице , поэтому угловая скорость результирующего вектора    численно  равна угловой частоте  переменного тока.                                        

В реальной многополюсной машине  поле вращается медленнее в  раз, что необходимо учитывать при расчете характеристик реальных асинхронных двигателей.

Сравнивая потокосцепления   и   c  аналогичными выражениями для двухфазной обобщенной модели можно заметить, что  трехфазная система также образует вращающееся магнитное поле, но результирующий вектор потокосцепления в 1,5 раза превышает потокосцепление отдельных фаз. Это означает,   что для соблюдения эквивалентности преобразования необходимо учитывать согласующий коэффициент К_С. Обратное двухфазно-трехфазное преобразование осуществляется с помощью изображающего вектора по (2.16).

В трехфазной системе изображающий вектор совпадает по направлению с  результирующим, но отличается от него по величине 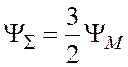. Множитель 3/2 будет встречаться в тех формулах, где из уравнений, записанных для изображающего вектора, необходимо сделать  выводы о переменных, зависящих от переменных трехфазного двигателя.