Частотное управление асинхронными двигателями. Законы частотного регулирования. Регулирование с постоянной мощностью, страница 2

Приведенные на рис. 1.2(а, б и с)  характеристики являются идеализированными, так как получены при пренебрежении падением напряжения на сопротивлении статора R₁.  При   двигатель работает в условиях мало отличающихся от номинальных. При дальнейшем уменьшении частоты  характеристики резко ухудшаются  из-за снижения потока, обусловленного падением напряжения на сопротивлениях статора.

Указанные законы могут быть использованы при небольших диапазонах регулирования скорости.

Другие законы частотного регулирования могут быть получены  при рассмотрении схемы замещения асинхронного двигателя, рис. 1.4.

                               

            1                             2                                 3                             4

.

                                               

                                                                              

0                                                                   

Рис.1-4

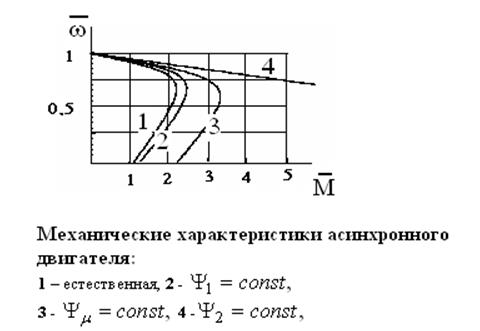
1. , - пропорциональный закон частотного управления;

2.      - закон постоянства полного потока:

3.       - закон постоянства рабочего потока  (потока  намагничивания);

4.          - закон постоянства потокосцепления   

ротора.

                     2.Математические модели асинхронного двигателя

2.1.  Обобщенная электрическая машина

В теории электрических машин часто пользуются математической моделью в виде обобщенной двухфазной электрической машины. Такая машина имеет по две обмотки на статоре и роторе, сдвинутые в пространстве на угол 90⁰.

Если такие обмотки питать переменными токами, сдвинутыми во времени на угол 90⁰ , в воздушном зазоре создается вращающееся магнитное поле.

При аналитическом описании процессов электромеханического преобразования энергии используются следующие допущения, позволяющие упростить модель:

- обмотки статора симметричны;

- поверхность статора и ротора  принимается гладкой, чем достигается постоянство магнитного сопротивления и собственных индуктивностей обмоток;

- напряжения и токи строго синусоидальны.

              

                              

  

           

      

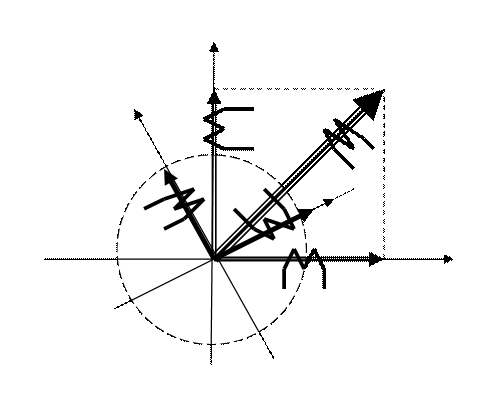
Рис.2-1

На рис.2-1 показана двухфазная модель электрической машины, у которой  оси координат  и  связаны с обмотками статора и неподвижны в пространстве, а оси  и  вращаются вместе с ротором.

   Если положить, что потокосцепления обмоток статора  равны и синусоидальны, то:                                             

                                                _,

                                                .                                           (2.1)

В пространстве каждое потокосцепление может быть представлено вектором, направленным вдоль  оси обмотки. Результирующее потокосцепление двух обмоток

                                                (2.2)

Поскольку векторы  и  ортогональны, то модуль вектора  будет равен

        (2.3)

т.е. в симметричной двухфазной магнитной системе модуль результирующего вектора является величиной постоянной и равной модулям потокосцепления фазных обмоток.

Для векторного сложения составляющих потока  запишем потокосцепление в комплексной форме,  совместив действительную ось с осью  , а мнимую - с осью , тогда

.

В показательной форме данное выражение будет иметь вид

                                   (2.4)

Умножение на  означает поворот вектора на угол .   Если угол  изменяется с постоянной скоростью , то вектор , не изменяясь во времени по модулю, вращается в пространстве с угловой скоростью , числено равной угловой частоте  тока статора .

Таким образом, система двух неподвижных обмоток статора, питаемых переменным током, может быть заменена одной вращающейся обмоткой, питаемой постоянным током, потокосцепление которой равно результирующему потокосцеплению.