Частотное управление асинхронными двигателями. Законы частотного регулирования. Регулирование с постоянной мощностью, страница 3

          Если результирующий вектор однозначно определяет потокосцепление в каждой обмотке статора,  его называют изображающим вектором. Для двухфазной машины результирующий вектор совпадает с изображающим.

Для перехода от эквивалентной системы обмоток и потокосцеплений перейти к реальной  достаточно спроектировать результирующий вектор на оси обмоток   и .

Как следует из рис.2-1,  эти проекции будут равны потокосцеплениям  и . При непрерывном вращении вектора его проекции будут отражать изменение потокосцеплений  и  во времени.

Аналогично может быть определен результирующий вектор потокосцепления ротора ,  при этом предполагается, что магнитная система ротора симметрична, токи синусоидальны и сдвинуты по фазе на угол 90⁰.

Цель применения результирующих векторов заключается в упрощении математического описания. Для двухфазной модели задача сводится к простейшему варианту электромеханического взаимодействия двух обмоток, одна из которых расположена на статоре, а другая на роторе.

По аналогии с потокосцеплением могут быть определены  результирующие векторы тока, эдс, напряжения.

Для обобщенной двухфазной машины уравнения ЭДС можно записать в виде:

                      (2.5)

Переменные в (2.5) представляют собой изображающие векторы напряжения, тока и потокосцепления, параметры ротора приведены к эквивалентным параметрам статора.

Потокосцепления статора и ротора создаются токами в  обеих обмотках, поэтому каждое потокосцепление является линейной комбинацией тока статора и приведенного тока ротора. Коэффициентами в этих уравнениях служат соответствующие индуктивности

                                  ,               (2.6)

где  и - собственные индуктивности обмоток статора и ротора; - взаимная индуктивность.

Найдем активную мощность, потребляемую обмоткой статора, как действительную часть произведения вектора напряжения на сопряженный вектор тока статора

.                                             (2.7)

Подставив   в (2.7)  напряжение         из (2.5),  получим

.                 (2.8)

Первое и второе слагаемые представляют собой потери в цепи статора и мощность, связанную с изменением энергии магнитного поля. Третье слагаемое  - электромагнитная мощность, равная произведению электромагнитного момента на синхронную скорость:

                        (2.9)

откуда может быть найден электромагнитный момент асинхронной машины

.                                  (2.10)

Электромагнитный момент может быть записан в другой форме. Для  этого обозначим  и  , тогда      

   , а выражение для момента  принимает вид:  

            .        (2.11)

В (2.9) и (2.10) момент выражен через параметры статора, однако во многих случаях момент удобнее вычислять через смешанные параметры статора и ротора.

Из (2.6) можно выразить потокосцепление статора через потокосцепление ротора

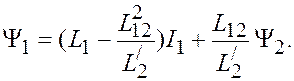
Подставив это значение в (2.10),  получим

                                                                        

,                   (2.12)

поскольку первое слагаемое в фигурных скобках равно нулю.

Могут быть получены и другие выражения для момента:

,

,

                                                                                               

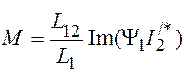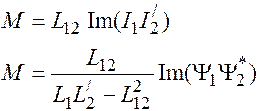
Делая вывод по данному разделу можно сказать, что выбор двухфазной машины в качестве обобщенной модели позволил в наиболее компактной и наглядной форме получить  математическое описание, отражающее основные особенности преобразования энергии  для широкого класса двигателей.

2.2  Трехфазно-двухфазное преобразование