Лекция 5 проф.
Содержание лекции 4.
Дано описание физической структуры и
принципа действия экстраполятора первого порядка (Э1), его модели,
характеристик и свойств. Описаны основы трех дискретных преобразований РФ.
Изложены основные свойства ![]()
![]() и
и![]() преобразований.
преобразований.
ГЛАВА 3. Структурные схемы. Передаточные функции ДСАУ.
3.1 Исходные положения
В ДСАУ (подразумеваем линейную дискретную систему) используются те же методы преобразования схем как в непрерывных системах (метод структурных схем и направленных графов). Но есть специфические особенностей структур и особые свойства таких устройств. Будем различать “типовые простейшие импульсные системы” и “нетиповые импульсные системы”.
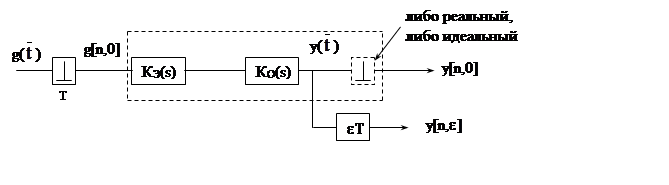
Рассмотрим типовую простейшую ИС (рис.1. 5.). Она должна иметь на входе и выходе ИИЭ, а внутри экстрополятор и непрервывный объект. Этот аналоговый объект должен быть, как правило, звеном САУ (интегратором, апериодическим, колебательным, реальным дифференцирующим, безинерционным).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Рис 1.5
Рис 1.5
На
входе и выходе типовой ИС формируются решётчатые функции. – Это очень важное
свойство! В аналитических моделях*) ДСАУ мы
обычно оперируем дискретными передаточными функциями
(ДПФ). Напомним, что ДПФ есть отношение изображенийвыходного сигнала y[n,
0] к входному - g]n, 0]. Поэтому
они должны быть одной математической формы (либо![]()
![]() или
или ![]() преобразований).
преобразований).
Если рассматривать
смещенные РФ y[n, ε], то физически они не существуют. Их получают выборкой
из непрерывного сигнала ![]() , включив элемент задержки и идеальный (фиктивный) ИИЭ. (См. Рис. 1.5.). Тогда
РФ
, включив элемент задержки и идеальный (фиктивный) ИИЭ. (См. Рис. 1.5.). Тогда
РФ
__________________________________________________________________
*)"Аналитической" здесь названа модельДСАУ, полученная в области изображений РФ и разностных уравнений. Такую модель нам привычнее и удобнее использовать при теоретических исследованиях систем. При исследовании же моделей ДСАУ на ЭВМ, (когда применяют пакетами MatLab, DS - 88 и др.), мы пользуемся имитационным моделированием их рабочих процессов во временной области, используя сами РФ и разностные уравнения. Постарайтесь уяснить и помнить это при изучении курса
выхода y[n,ε] будет смещена относительно g[n,0] на величину ε или εT, если у них равный интервал квантования.
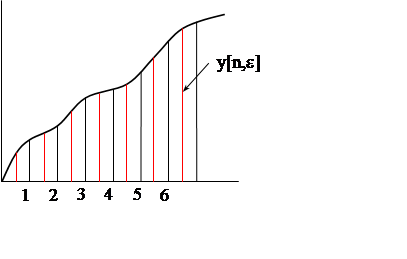

Рис..2.5
3.2 Последовательное соединение простейших импульсных систем
 Рис. 3.5.
Рис. 3.5.
Несмещенная передаточная функция последовательно соединенных типовых ИС (см. рис. 3.5.):
![]() .
(1.5.)
.
(1.5.)
Смещению подвергается только последний сигнал. Поэтому смещенная ДПФ того же соединения будет:
![]() .
(2.5.)
.
(2.5.)
Запись для z-преобразования действительна и для w-преобразования:
![]() при замене
при замене ![]() в
в 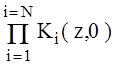
Этот материал изложен во всех основополагающих работах по теории ДСАУ[1, 2, 3, 6, 9 и др.]. Но реальной практической ценности он почти не имеет. Дело заключается в том, что структура рис 3. 5 явно "надумана". В структуре реальной ДСАУ последовательно используют, как правило, один экстраполятор. Тогда и "дробить" информацию многочисленными импульсными элементами не только бессмысленно, но и вредно!
3.3 Параллельное соединение типовых импульсных систем
Эти схемы реальны. Ниже приводим формулы для получения ДПФ таких соединений без пояснений, поскольку они аналогичны и для моделей аналоговых систем.
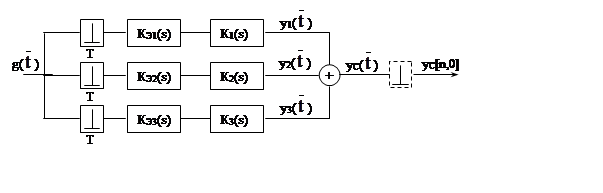
Рис.4.5.
Несмещенная передаточная функция параллельно соединенных типовых ИС (см.: рис.4. 5.) будет:
![]() .
(3.5.)
.
(3.5.)
Смещенная ДПФ того же соединения выглядит так:
![]() .
(4.5.)
.
(4.5.)
3.4 Преобразование нетиповых структур ДСАУ
На практике чаще встречается структура, изображенная на рис. 5.5.
Такие схемы реальны, нужно внимательно отнестись к излагаемым методам их преобразования, хотя они могут потребовать больших рутинных работ.
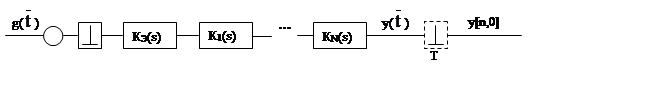
Рис. 5. 5.
![]() (5.5.)
(5.5.)
![]() ,
, 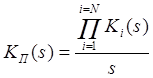 ,
, ![]()
Следовательно:
![]() ,
(6.5.)
,
(6.5.)
так
как ![]() , где
К(s) с римскими индексами – это новые аналоговые передаточные
функции, не соответствующие K(s) с арабскими индексами. Эта формула показывает возможность преобразования
произведения ПФ в сумму.
, где
К(s) с римскими индексами – это новые аналоговые передаточные
функции, не соответствующие K(s) с арабскими индексами. Эта формула показывает возможность преобразования
произведения ПФ в сумму.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.