Описание физической структуры и принципа действия экстраполятора первого порядка, его модели, характеристик и свойств, страница 2

В математике задачу преобразования произведения функций в суммувыполняют методом "разложения на элементарные дроби".При этом нужно соблюдать одинаковую размерность слагаемых.

Для смещенных ДПФ выражение (6.5.) приобретает иной вид:

                                        (7.5.)

Примечание 1.  Задача. Найти ДПФ двух апериодических звеньев, соединенных как типовые ИС и нетиповые ИС?

Решение. Передаточные функции звеньев будут:

Их ДПФ с экстраполятором нулевого порядка, (воспользовавшись специальными таблицами преобразований K(s) форм функций в K(z, 0) формы функции), найдем в таком виде:

Перемножая полученные ДПФ по формуле (1.5.), получим:

(см. рис. 3.5.).                                             (1.5.) ¹

Найдем теперь соединение тех же звеньев в "нетиповую ИС".

 (**)

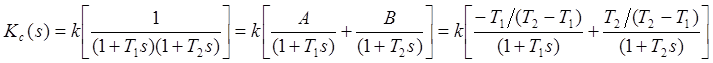Преобразуя выражение (*.*) по формуле (6.5), получим:

      (6.5)¹

Сопоставляя выражения (1.5)¹ и (6.5)¹, нетрудно заметить различия в содержании полиномов числителей этих ДПФ (хотя знаменатели равны). Следовательно будет иной  динамика и устойчивостть "типовых" и "нетиповых" ИС. Ещё раз напомним ,что реально используются как те, так и другие структуры ДСАУ.

Преобразование нетиповой структуры при наличии экстраполятора первого порядке ещё сложнее. Сначала его запишем, аналогично (6.5.), в общем виде

,                                                                         (8.5)

где  

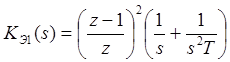
Затем примем:,  

Следовательно выражение (8.5.) разрешится в такой форме:

.                                                                (9.5.)

Здесь, в первую очередь, необходимо вычислить неопределенные коэффициенты А B, C и D в нижеследующих равенствах:

., а затем найти . Далее преобразования завершаются в (9.5.) подстановкой туда найденных форм с помощью специальных таблиц или "вычетов".

Аналогично можно воспользоваться и w-преобразованием.

3.5 Передаточная функция замкнутых систем

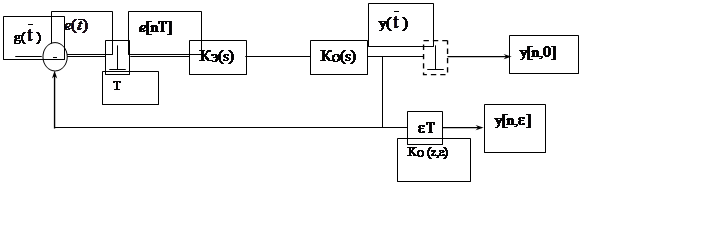
Передаточные функции замкнутых систем разнообразны. Это зависит от структуры физической модели ДСАУ. Ниже приводится одна из структур.

E (z,0)

KO (z, 0)

Рис. 6.5.

Здесь (рис. 6.5.) использованы один реальный и два идеальных ИЭ²⁾. Обозначим . Это будет несмещенная ДПФ объекта ("приведенной" разомкнутой системы) и смещенная ДПФ объекта .

Для замкнутой САУ получим ДПФ в таких видах:

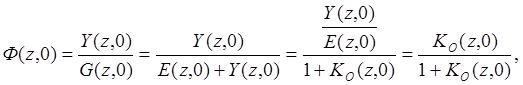несмещенная       (10.5.)

. смещенная                               (11.5.)

Устойчивость ДСАУ определяется по знаменателю ДПФ: 1+ K(z,0). Это выражение от смещения не зависит. Тогда возникает резонный вопрос. Зачем нужны модели более сложных смещенных РФ и ДПФ? Поясним необходимость смещенных и несмещенных РФ и ДПФ на одном примере.

В реальных ДСАУ, при определенной структуре и интервале квантования, может возникнуть режим "скрытых колебаний", который нельзя обнаружить выборкой несмещенной РФ (см. рис.7.5.). Притом, что огибающая кривая  является неустойчивой (колебательной, расходящейся).

Если же огибающую строить по смещенным и несмещенным значениям РФ, то режим “скрытых колебании”, обнаруживается. Попутно заметим, что аналитическую оценку устойчивости таких систем определить очень сложно. В последующих лекциях это будет сделано.

 

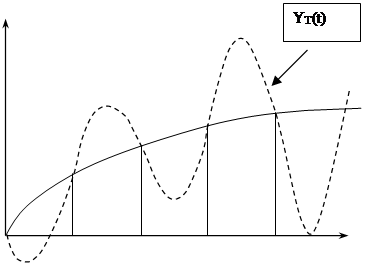Рис.7.5.

²⁾Примечание 2. Отметим ещё, что на выходе линии задержки "εТ" помещен фиктивный квантователь для смещенного сигнала y[n, εT], чтобы получить ДПФ , как и для РФ - y[n, 0]. Суть вопроса состоит в том, что схема, изображенная на рис.6. 5, является расчетной моделью, а не реальной структурой. Она предназначена для  аналитических, а не имитационных исследований ДСАУ. Поэтому для расчетной модели (схемы) оказывается неважным, что обе РФ выхода y[n, 0] и

y[n, εT] фиктивны. Хотя y[n, 0]присутствует в модели как реальная функция, представленная разностью двух реальных дискретных сигналов: y[n, 0] =g[n, 0] - e [n, 0].

Смещенную же РФ y[n, εT], как реальную (или вычисляемую) величину, не найти в схеме рис.6. 5.,без её структурной перестройки.

Скорректировано 03.03.09.